AI For Trading:Portfolio Optimization (43)

What is Optimization?

Second-order condition(二阶条件)

In the previous problem, we cheated a little. We knew the shape of the function, and we knew its orientation from our plot, so when we found the point where the derivative equaled 0, we knew we had found the minimum.
在上一个问题中，我们作弊了一点。我们知道函数的形状，并且我们从绘图中知道它的方向，所以当我们找到导数等于0的点时，我们知道我们找到了最小值。

However, in general, points where the derivative equals 0 could be minima, maxima, or saddle points. To distinguish between these cases, we need to check the function's curvature around the point in question. We do this using the second derivative of the function. For a function of one variable, the rule is:
但是，通常，导数等于0的点可以是最小值，最大值或鞍点。为了区分这些情况，我们需要检查函数在所讨论的点周围的曲率。我们使用函数的二阶导数来做到这一点。对于一个变量的函数，规则是：

The second derivative is positive for all x, which means the function's slope is increasing everywhere, hence the function's curvature is upward everywhere. So we can be confident that the point we found is a minimum.
对于所有x，二阶导数都是正的，这意味着函数的斜率在任何地方都在增加，因此函数的曲率在任何地方都是向上的。因此，我们可以确信我们发现的观点是最小的。

For a function of two variables, the rule must change a bit. We construct the matrix of second-order partial derivatives:
对于两个变量的函数，规则必须改变一点。我们构造了二阶偏导数矩阵：

Two-Asset Portfolio Optimization(双资产组合优化)

Derivation of Optimal Weights on a Two-Asset Portfolio

So how do we set up the portfolio optimization problem? In general, we know that we want high returns and low variance of returns, and that the weights on each asset in our portfolio should sum to 1.
那么我们如何设置投资组合优化问题呢？一般而言，我们知道我们希望获得高回报和低回报差异，并且我们投资组合中每项资产的权重应该总和为1。

Let's again consider a portfolio a portfolio with 2 assets in it, Stock A and Stock B. We want to solve for the weight on each asset, \(x_A\) and \(x_B\).

Our objective function for this problem is the expression for the portfolio variance:
我们针对这个问题的目标函数是投资组合差异的表达式：

This is what we will seek to minimize.

Our only constraint is:

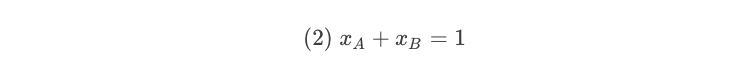
It turns out that this is a problem we can solve analytically. If we substitute (2)(2) into (1)(1), we will get a function of a single variable:

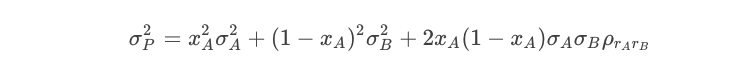
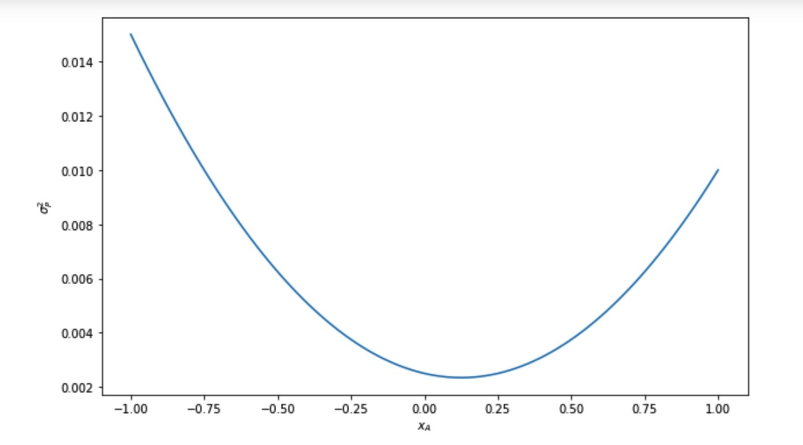
Cool, it's a parabola. So now we see that we are looking for the bottom of that parabola again.
很酷，这是一个抛物线。所以现在我们看到我们再次寻找抛物线的底部。

So, since this is a problem in only one variable, \(x_A\) , let's take the derivative with respect to \(x_A\) , and solve for the value of \(x_A\) that makes the resulting expression equal 0:

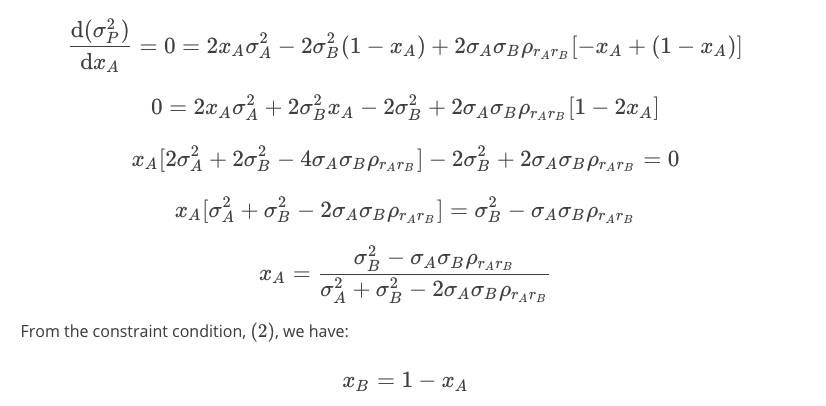
Now we know the portfolio weights. You can see that they are only dependent on the standard deviations (标准偏差)of Stock A and B, and their covariance(协方差). If we wanted to know the expected portfolio mean, we only have to remember that it is the weighted sum of the individual portfolio means:

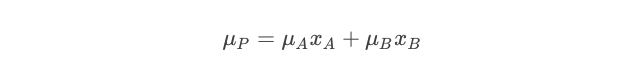
To be sure our solution is a minimum, we should check the second-order condition. We will leave this as an exercise to you.

Quize:Portfolio Optimization with 2 Stocks

练习题

Let’s say we want to construct a portfolio containing 2 stocks, Stock 1 and Stock 2.

Stock 1: Expected return=15%, Volatility=10%

Stock 2: Expected return=10%, Volatility=5%

Correlation between Stock A and B = 0.25
What weights on Stocks 1 and 2, \(x_1\) and \(x_2\) , will give the minimum variance portfolio?
会给出最小的方差组合吗？

Formulating Portfolio Optimization Problems

Formulating Portfolio Optimization Problems

So far, we've discussed one way to formulate a portfolio optimization problem. We learned to set the portfolio variance as the objective function, while imposing the constraint that the portfolio weights should sum to 1. However, in practice you may frame the problem a little differently. Let's talk about some of the different ways to set up a portfolio optimization problem.

到目前为止，我们已经讨论了制定投资组合优化问题的一种方法。我们学会了将投资组合方差设置为目标函数，同时强加投资组合权重应该总和为1的约束。但是，在实践中，您可能会稍微区别对待问题。我们来谈谈建立投资组合优化问题的一些不同方法。

Common Constraints

There are several common constraints that show up in these problems. Earlier, we were allowing our portfolio weights to be negative or positive, as long as they summed to 1. If a weight turned out to be negative, we would consider the absolute value of that number to be the size of the short position to take on that asset. If your strategy does not allow you to take short positions, your portfolio weights will all need to be positive numbers. In order to enforce this in the optimization problem, you would add the constraint that every \(x_i\) in the \(\mathbf{x}\) vector is positive.

在这些问题中出现了几种常见的约束。早些时候，我们允许我们的投资组合权重为负或正，只要它们总和为1.如果权重结果为负数，我们会将该数字的绝对值视为该资产的空头头寸。如果您的策略不允许您做空头寸，您的投资组合权重都需要为正数。

Maximizing Portfolio Return(最大化投资组合回报)

We can also flip the problem around by maximizing returns instead of minimizing variance. Instead of minimizing variance, it often makes sense to impose a constraint on the variance in order to manage risk. Then you could maximize mean returns, which is equivalent to minimizing the negative mean returns. This makes sense when your employer has told you, “I want the best return possible, but you must limit your losses to pp percent!”

我们还可以通过最大化回报而不是最小化方差来解决问题。为了管理风险，对方差施加约束通常是有意义的，而不是最小化方差。那么你可以最大化平均回报，这相当于最小化负平均回报。当你的雇主告诉你，“我希望获得最好的回报，但你必须将你的损失限制在p％！”这是有道理的。

Maximizing Portfolio Return And Minimizing Portfolio Variance

Indeed, you could also create an objective function that both maximizes returns and minimizes variance, and controls the tradeoff between the two goals with a parameter, b. In this case, you have two terms in your objective function, one representing the portfolio mean, and one representing the portfolio variance, and the variance term is multiplied by b.

实际上，您还可以创建一个目标函数，既可以使回报最大化又可以最小化方差，并通过参数b控制两个目标之间的权衡。
在这种情况下，您的目标函数中有两个项，一个代表投资组合均值，一个代表投资组合方差，方差项乘以b。

How does one determine the parameter bb? Well, it’s very dependent on the individual and the situation, and depends on the level of risk aversion appropriate. It basically represents how much percent return you are willing to give up for each unit of variance you take on.

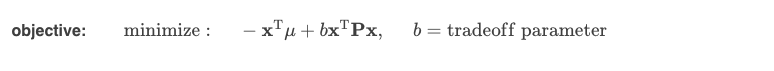
A Math Note: the L2-Norm

There’s another way to formulate an optimization objective that relies on a new piece of notation, so I’ll just take a moment to explain that now. Say we just want to minimize the difference between two quantities. Then we need a measure of the difference, but generalized into many dimensions. For portfolio optimization problems, each dimension is an asset in the portfolio. When we want to measure the distance between two vectors, we use something called the Euclidean norm or L2-norm. This is just the square root of the squared differences of each of the vectors’ components. We write it with double bars and a 2 subscript.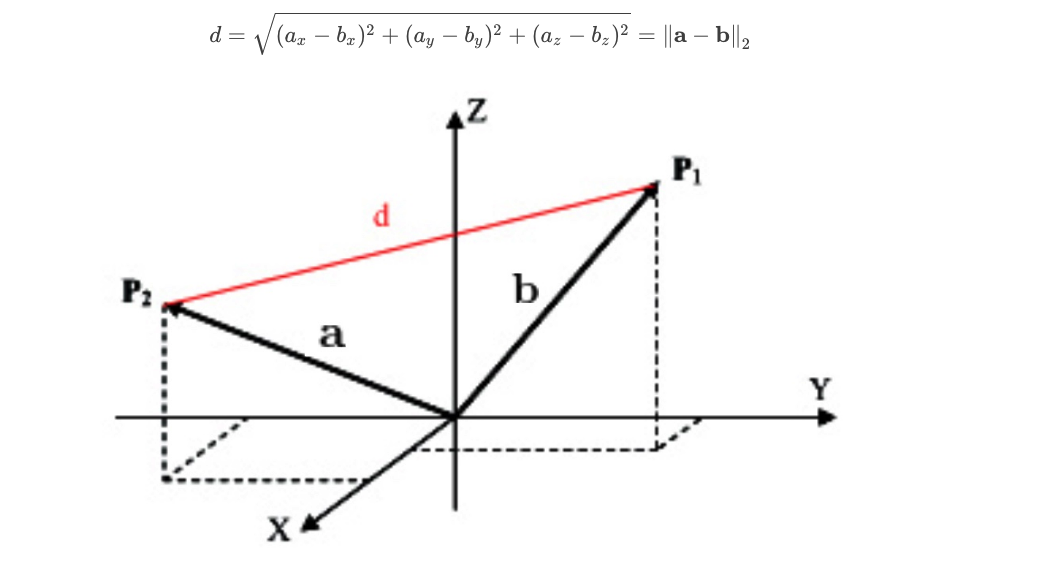

Minimizing Distance to a Set of Target Weights

ack to portfolio optimization! One way to formulate an optimization problem is to use the L2 norm and minimize the difference between your vector of portfolio weights and a set of predefined target portfolio weights \(\mathbf{x}^*\)
. The goal would be to get the weights as close as possible to the set of target weights while respecting a set of constraints. As an example, these target weights might be values thought to be proportional to future returns for each asset, in other words, an alpha vector.

Tracking an Index

练习题

Let's say you have two terms in your optimization objective, and lambda is multiplied to the second term. If you choose a larger lambda, do you think this causes the optimization to be influenced more by the goal of minimizing the first term or the goal of minimizing the second term?

That's correct! The optimization objective consists of a sum of two quantities: 1) the first term, and 2) the second term times lambda. If lambda is very large, the second quantity in the sum will be larger, and will have more influence on the overall size of the sum. If you choose a larger lambda for the second quantity, the overall optimization will be influenced more by the second quantity.

为者常成，行者常至