AI For Trading: Portfolio Variance (54)
Portfolio Variance
import sys
!{sys.executable} -m pip install -r requirements.txtRequirement already satisfied: numpy==1.14.5 in /opt/conda/lib/python3.6/site-packages (from -r requirements.txt (line 1))
Requirement already satisfied: pandas==0.18.1 in /opt/conda/lib/python3.6/site-packages (from -r requirements.txt (line 2))
Requirement already satisfied: plotly==2.2.3 in /opt/conda/lib/python3.6/site-packages (from -r requirements.txt (line 3))
Requirement already satisfied: scikit-learn==0.19.1 in /opt/conda/lib/python3.6/site-packages (from -r requirements.txt (line 4))
Requirement already satisfied: six==1.11.0 in /opt/conda/lib/python3.6/site-packages (from -r requirements.txt (line 5))
Requirement already satisfied: zipline===1.2.0 in /opt/conda/lib/python3.6/site-packages (from -r requirements.txt (line 6))
Requirement already satisfied: python-dateutil>=2 in /opt/conda/lib/python3.6/site-packages (from pandas==0.18.1->-r requirements.txt (line 2))
Requirement already satisfied: pytz>=2011k in /opt/conda/lib/python3.6/site-packages (from pandas==0.18.1->-r requirements.txt (line 2))
[33mYou are using pip version 9.0.1, however version 18.1 is available.
You should consider upgrading via the 'pip install --upgrade pip' command.[0mimport numpy as np
import pandas as pd
import time
import os
import quiz_helper
import matplotlib.pyplot as plt%matplotlib inline
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (14, 8)data bundle
import os
import quiz_helper
from zipline.data import bundlesos.environ['ZIPLINE_ROOT'] = os.path.join(os.getcwd(), '..', '..','data','module_4_quizzes_eod')
ingest_func = bundles.csvdir.csvdir_equities(['daily'], quiz_helper.EOD_BUNDLE_NAME)
bundles.register(quiz_helper.EOD_BUNDLE_NAME, ingest_func)
print('Data Registered')Data RegisteredBuild pipeline engine
from zipline.pipeline import Pipeline
from zipline.pipeline.factors import AverageDollarVolume
from zipline.utils.calendars import get_calendar
universe = AverageDollarVolume(window_length=120).top(500)
trading_calendar = get_calendar('NYSE')
bundle_data = bundles.load(quiz_helper.EOD_BUNDLE_NAME)
engine = quiz_helper.build_pipeline_engine(bundle_data, trading_calendar)View Data
With the pipeline engine built, let's get the stocks at the end of the period in the universe we're using. We'll use these tickers to generate the returns data for the our risk model.
universe_end_date = pd.Timestamp('2016-01-05', tz='UTC')
universe_tickers = engine\
.run_pipeline(
Pipeline(screen=universe),
universe_end_date,
universe_end_date)\
.index.get_level_values(1)\
.values.tolist()
universe_tickers[Equity(0 [A]),
Equity(1 [AAL]),
Equity(2 [AAP]),
Equity(3 [AAPL]),
Equity(4 [ABBV]),
Equity(5 [ABC]),
Equity(6 [ABT]),
Equity(7 [ACN]),
Equity(8 [ADBE]),
Equity(9 [ADI]),
Equity(10 [ADM]),
Equity(11 [ADP]),
Equity(12 [ADS]),
Equity(13 [ADSK]),
Equity(14 [AEE]),
Equity(15 [AEP]),
Equity(16 [AES]),
Equity(17 [AET]),
Equity(18 [AFL]),
Equity(19 [AGN]),
Equity(20 [AIG]),
Equity(21 [AIV]),
Equity(22 [AIZ]),
Equity(23 [AJG]),
Equity(24 [AKAM]),
Equity(25 [ALB]),
Equity(26 [ALGN]),
Equity(27 [ALK]),
Equity(28 [ALL]),
Equity(29 [ALLE]),
Equity(30 [ALXN]),
Equity(31 [AMAT]),
Equity(32 [AMD]),
Equity(33 [AME]),
Equity(34 [AMG]),
Equity(35 [AMGN]),
...
Equity(488 [ZBH]),
Equity(489 [ZION]),
Equity(490 [ZTS])]len(universe_tickers)490from zipline.data.data_portal import DataPortal
data_portal = DataPortal(
bundle_data.asset_finder,
trading_calendar=trading_calendar,
first_trading_day=bundle_data.equity_daily_bar_reader.first_trading_day,
equity_minute_reader=None,
equity_daily_reader=bundle_data.equity_daily_bar_reader,
adjustment_reader=bundle_data.adjustment_reader)Get pricing data helper function
from quiz_helper import get_pricingget pricing data into a dataframe
returns_df = \
get_pricing(
data_portal,
trading_calendar,
universe_tickers,
universe_end_date - pd.DateOffset(years=5),
universe_end_date)\
.pct_change()[1:].fillna(0) #convert prices into returns
returns_df| Equity(0 [A]) | Equity(1 [AAL]) | Equity(2 [AAP]) | Equity(3 [AAPL]) | Equity(4 [ABBV]) | Equity(5 [ABC]) | Equity(6 [ABT]) | Equity(7 [ACN]) | Equity(8 [ADBE]) | Equity(9 [ADI]) | ... | Equity(481 [XL]) | Equity(482 [XLNX]) | Equity(483 [XOM]) | Equity(484 [XRAY]) | Equity(485 [XRX]) | Equity(486 [XYL]) | Equity(487 [YUM]) | Equity(488 [ZBH]) | Equity(489 [ZION]) | Equity(490 [ZTS]) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011-01-07 00:00:00+00:00 | 0.008437 | 0.014230 | 0.026702 | 0.007146 | 0.000000 | 0.001994 | 0.004165 | 0.001648 | -0.007127 | -0.005818 | ... | -0.001838 | -0.005619 | 0.005461 | -0.004044 | -0.013953 | 0.000000 | 0.012457 | -0.000181 | -0.010458 | 0.000000 |
| 2011-01-10 00:00:00+00:00 | -0.004174 | 0.006195 | 0.007435 | 0.018852 | 0.000000 | -0.005714 | -0.008896 | -0.008854 | 0.028714 | 0.002926 | ... | 0.000947 | 0.007814 | -0.006081 | 0.010466 | 0.009733 | 0.000000 | 0.001440 | 0.007784 | -0.017945 | 0.000000 |
| 2016-01-05 00:00:00+00:00 | 0.004058 | -0.009541 | -0.006830 | -0.025054 | -0.004169 | 0.014629 | -0.000247 | 0.005207 | 0.004023 | -0.007347 | ... | 0.002098 | 0.014863 | 0.008511 | 0.020390 | -0.001957 | -0.000286 | -0.002495 | 0.020820 | -0.010853 | 0.015647 |
1256 rows 490 columns
Let's look at a two stock portfolio
Let's pretend we have a portfolio of two stocks. We'll pick Apple and Microsoft in this example.
aapl_col = returns_df.columns[3]
msft_col = returns_df.columns[312]
asset_return_1 = returns_df[aapl_col].rename('asset_return_aapl')
asset_return_2 = returns_df[msft_col].rename('asset_return_msft')
asset_return_df = pd.concat([asset_return_1,asset_return_2],axis=1)
asset_return_df.head(2)| asset_return_aapl | asset_return_msft | |
|---|---|---|
| 2011-01-07 00:00:00+00:00 | 0.007146 | -0.007597 |
| 2011-01-10 00:00:00+00:00 | 0.018852 | -0.013311 |
Factor returns
Let's make up a "factor" by taking an average of all stocks in our list. You can think of this as an equal weighted index of the 490 stocks, kind of like a measure of the "market". We'll also make another factor by calculating the median of all the stocks. These are mainly intended to help us generate some data to work with. We'll go into how some common risk factors are generated later in the lessons.
Also note that we're setting axis=1 so that we calculate a value for each time period (row) instead of one value for each column (assets).
factor_return_1 = returns_df.mean(axis=1)
factor_return_2 = returns_df.median(axis=1)
factor_return_l = [factor_return_1, factor_return_2]Factor exposures
Factor exposures refer to how "exposed" a stock is to each factor. We'll get into this more later. For now, just think of this as one number for each stock, for each of the factors.
from sklearn.linear_model import LinearRegression"""
For now, just assume that we're calculating a number for each
stock, for each factor, which represents how "exposed" each stock is
to each factor.
We'll discuss how factor exposure is calculated later in the lessons.
"""
def get_factor_exposures(factor_return_l, asset_return):
lr = LinearRegression()
X = np.array(factor_return_l).T
y = np.array(asset_return.values)
lr.fit(X,y)
return lr.coef_factor_exposure_l = []
for i in range(len(asset_return_df.columns)):
factor_exposure_l.append(
get_factor_exposures(factor_return_l,
asset_return_df[asset_return_df.columns[i]]
))
factor_exposure_a = np.array(factor_exposure_l)print(f"factor_exposures for asset 1 {factor_exposure_a[0]}")
print(f"factor_exposures for asset 2 {factor_exposure_a[1]}")factor_exposures for asset 1 [ 1.35101534 -0.58353198]
factor_exposures for asset 2 [-0.2283345 1.16364007]Variance of stock 1
Calculate the variance of stock 1.
$\textrm{Var}(r{1}) = \beta{1,1}^2 \textrm{Var}(f{1}) + \beta{1,2}^2 \textrm{Var}(f{2}) + 2\beta{1,1}\beta{1,2}\textrm{Cov}(f{1},f{2}) + \textrm{Var}(s{1})$
factor_exposure_1_1 = factor_exposure_a[0][0]
factor_exposure_1_2 = factor_exposure_a[0][1]
common_return_1 = factor_exposure_1_1 * factor_return_1 + factor_exposure_1_2 * factor_return_2
specific_return_1 = asset_return_1 - common_return_1covm_f1_f2 = np.cov(factor_return_1,factor_return_2,ddof=1) #this calculates a covariance matrix
# get the variance of each factor, and covariances from the covariance matrix covm_f1_f2
var_f1 = covm_f1_f2[0,0]
var_f2 = covm_f1_f2[1,1]
cov_f1_f2 = covm_f1_f2[0][1]
# calculate the specific variance.
var_s_1 = np.var(specific_return_1,ddof=1)
# calculate the variance of asset 1 in terms of the factors and specific variance
var_asset_1 = (factor_exposure_1_1**2 * var_f1) + \
(factor_exposure_1_2**2 * var_f2) + \
2 * (factor_exposure_1_1 * factor_exposure_1_2 * cov_f1_f2) + \
var_s_1
print(f"variance of asset 1: {var_asset_1:.8f}")variance of asset 1: 0.00028209Variance of stock 2
Calculate the variance of stock 2.
$\textrm{Var}(r{2}) = \beta{2,1}^2 \textrm{Var}(f{1}) + \beta{2,2}^2 \textrm{Var}(f{2}) + 2\beta{2,1}\beta{2,2}\textrm{Cov}(f{1},f{2}) + \textrm{Var}(s{2})$
factor_exposure_2_1 = factor_exposure_a[1][0]
factor_exposure_2_2 = factor_exposure_a[1][1]
common_return_2 = factor_exposure_2_1 * factor_return_1 + factor_exposure_2_2 * factor_return_2
specific_return_2 = asset_return_2 - common_return_2# Notice we already calculated the variance and covariances of the factors
# calculate the specific variance of asset 2
var_s_2 = np.var(specific_return_2,ddof=1)
# calcualte the variance of asset 2 in terms of the factors and specific variance
var_asset_2 = (factor_exposure_2_1**2 * var_f1) + \
(factor_exposure_2_2**2 * var_f2) + \
(2 * factor_exposure_2_1 * factor_exposure_2_2 * cov_f1_f2) + \
var_s_2
print(f"variance of asset 2: {var_asset_2:.8f}")variance of asset 2: 0.00021856Covariance of stocks 1 and 2
Calculate the covariance of stock 1 and 2.
$\textrm{Cov}(r{1},r{2}) = \beta{1,1}\beta{2,1}\textrm{Var}(f{1}) + \beta{1,1}\beta{2,2}\textrm{Cov}(f{1},f{2}) + \beta{1,2}\beta{2,1}\textrm{Cov}(f{1},f{2}) + \beta{1,2}\beta{2,2}\textrm{Var}(f{2})$
# TODO: calculate the covariance of assets 1 and 2 in terms of the factors
cov_asset_1_2 = (factor_exposure_1_1 * factor_exposure_2_1 * var_f1) + \
(factor_exposure_1_1 * factor_exposure_2_2 * cov_f1_f2) + \
(factor_exposure_1_2 * factor_exposure_2_1 * cov_f1_f2) + \
(factor_exposure_1_2 * factor_exposure_2_2 * var_f2)
print(f"covariance of assets 1 and 2: {cov_asset_1_2:.8f}")covariance of assets 1 and 2: 0.00007133Quiz 1: calculate portfolio variance
We'll choose stock weights for now (in a later lesson, you'll learn how to use portfolio optimization that uses alpha factors and a risk factor model to choose stock weights).
$\textrm{Var}(rp) = x{1}^{2} \textrm{Var}(r1) + x{2}^{2} \textrm{Var}(r2) + 2x{1}x{2}\textrm{Cov}(r{1},r_{2})$
weight_1 = 0.60
weight_2 = 0.40
# TODO: calculate portfolio variance
var_portfolio = weight_1**2 * var_asset_1 + \
weight_2**2 * var_asset_2 + \
2*weight_1*weight_2*cov_asset_1_2
print(f"variance of portfolio is {var_portfolio:.8f}")variance of portfolio is 0.00017076Quiz 2: Do it with Matrices!
Create matrices $\mathbf{F}$, $\mathbf{B}$ and $\mathbf{S}$, where
$\mathbf{F}= \begin{pmatrix}
\textrm{Var}(f_1) & \textrm{Cov}(f_1,f_2) \\
\textrm{Cov}(f_2,f_1) & \textrm{Var}(f_2)
\end{pmatrix}$
is the covariance matrix of factors,
$\mathbf{B} = \begin{pmatrix}
\beta_{1,1}, \beta_{1,2}\\
\beta_{2,1}, \beta_{2,2}
\end{pmatrix}$
is the matrix of factor exposures, and
$\mathbf{S} = \begin{pmatrix}
\textrm{Var}(s_i) & 0\\
0 & \textrm{Var}(s_j)
\end{pmatrix}$
is the matrix of specific variances.
$\mathbf{X} = \begin{pmatrix}
x_{1} \\
x_{2}
\end{pmatrix}$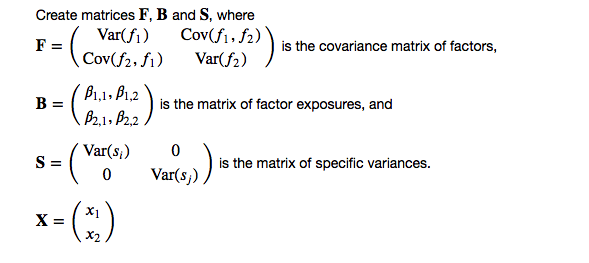
Concept Question
What are the dimensions of the $\textrm{Var}(r_p)$ portfolio variance? Given this, when choosing whether to multiply a row vector or a column vector on the left and right sides of the $\mathbf{BFB}^T$, which choice helps you get the dimensions of the portfolio variance term?
In other words:
Given that $\mathbf{X}$ is a column vector, which makes more sense?
$$\mathbf{X}^T(\mathbf{BFB}^T + \mathbf{S})\mathbf{X}$$ ?
or
$$\mathbf{X}(\mathbf{BFB}^T + \mathbf{S})\mathbf{X}^T$$ ?
Answer 2
Since the portfolio variance is 1 by 1 (it's a scalar), we want the matrix multiplications to create a 1 by 1 output as well. This means we should put the row vector
$\mathbf{X}^T = \begin{pmatrix}
x_{i} & x_{j}
\end{pmatrix}$
On the left, and put the column vector
$\mathbf{X} = \begin{pmatrix}
x_{i}\\
x_{j}
\end{pmatrix}$
On the right.
So we should use:
$\mathbf{X}^T(\mathbf{BFB}^T + \mathbf{S})\mathbf{X}$ ? 
Quiz 3: Calculate portfolio variance using matrices
# TODO: covariance matrix of factors
F = covm_f1_f2
Farray([[1.02562520e-04, 9.79887017e-05],
[9.79887017e-05, 9.44523986e-05]])# TODO: matrix of factor exposures
B = factor_exposure_a
Barray([[ 1.35101534, -0.58353198],
[-0.2283345 , 1.16364007]])# TODO: matrix of specific variances
S = np.diag([var_s_1,var_s_2])
Sarray([[0.00021723, 0. ],
[0. , 0.00013739]])Hint for column vectors
Try using reshape
# TODO: make a column vector for stock weights matrix X
X = np.array([weight_1,weight_2]).reshape(2,1)
Xarray([[0.6],
[0.4]])# TODO: covariance matrix of assets
var_portfolio = X.T.dot(B.dot(F).dot(B.T) + S).dot(X)
print(f"portfolio variance is \n{var_portfolio[0][0]:.8f}")portfolio variance is
0.00017076为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



