AI For Trading:PCA as A Factor Model (59)
PCA as a Factor Model - Coding Exercises
Introduction
As we learned in the previous lessons, we can use PCA to create a factor model of risk. Our risk factor model represents the return as:
$$
\textbf{r} = \textbf{B}\textbf{f} + \textbf{s}
$$
where $\textbf{r}$ is a matrix containing the asset returns, $\textbf{B}$ is a matrix representing the factor exposures, $\textbf{f}$ is the matrix of factor returns, and $\textbf{s}$ is the idiosyncratic risk (also known as the company specific risk).
In this notebook, we will use real stock data to calculate:
- The Factor Exposures (Factor Betas) $\textbf{B}$
- The Factor Returns $\textbf{f}$
- The Idiosyncratic Risk Matrix $\textbf{S}$
- The Factor Covariance Matrix $\textbf{F}$
We will then combine these quantities to create our Risk Model.
Install Packages
import sys
!{sys.executable} -m pip install -r requirements.txtCollecting zipline===1.3.0 (from -r requirements.txt (line 1))
Downloading https://files.pythonhosted.org/packages/be/59/8c5802a7897c1095fdc409fb557f04df8f75c37174e80d2ba58c8d8a6488/zipline-1.3.0.tar.gz (2.5MB)
[K 100% |████████████████████████████████| 2.5MB 189kB/s eta 0:00:01 17% |█████▋ | 430kB 6.6MB/s eta 0:00:01
[?25hRequirement already satisfied: pip>=7.1.0 in /opt/conda/lib/python3.6/site-packages (from zipline===1.3.0->-r requirements.txt (line 1))Get Returns
In this notebook, we will get the stock returns using Zipline and data from Quotemedia, just as we learned in previous lessons. The function get_returns(start_date, end_date) in the utils module, gets the data from the Quotemedia data bundle and produces the stock returns for the given start_date and end_date. You are welcome to take a look at the utils module to see how this is done.
In the code below, we use utils.get_returns funtion to get the returns for stock data between 2011-01-05 and 2016-01-05. You can change the start and end dates, but if you do, you have to make sure the dates are valid trading dates.
import utils
# Get the returns for the fiven start and end date. Both dates must be valid trading dates
returns = utils.get_returns(start_date='2011-01-05', end_date='2016-01-05')
# Display the first rows of the returns
returns.head()| Equity(0 [A]) | Equity(1 [AAL]) | Equity(2 [AAP]) | Equity(3 [AAPL]) | Equity(4 [ABBV]) | Equity(5 [ABC]) | Equity(6 [ABT]) | Equity(7 [ACN]) | Equity(8 [ADBE]) | Equity(9 [ADI]) | ... | Equity(481 [XL]) | Equity(482 [XLNX]) | Equity(483 [XOM]) | Equity(484 [XRAY]) | Equity(485 [XRX]) | Equity(486 [XYL]) | Equity(487 [YUM]) | Equity(488 [ZBH]) | Equity(489 [ZION]) | Equity(490 [ZTS]) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011-01-07 00:00:00+00:00 | 0.008437 | 0.014230 | 0.026702 | 0.007146 | 0.0 | 0.001994 | 0.004165 | 0.001648 | -0.007127 | -0.005818 | ... | -0.001838 | -0.005619 | 0.005461 | -0.004044 | -0.013953 | 0.0 | 0.012457 | -0.000181 | -0.010458 | 0.0 |
| 2011-01-10 00:00:00+00:00 | -0.004174 | 0.006195 | 0.007435 | 0.018852 | 0.0 | -0.005714 | -0.008896 | -0.008854 | 0.028714 | 0.002926 | ... | 0.000947 | 0.007814 | -0.006081 | 0.010466 | 0.009733 | 0.0 | 0.001440 | 0.007784 | -0.017945 | 0.0 |
| 2011-01-11 00:00:00+00:00 | -0.001886 | -0.043644 | -0.005927 | -0.002367 | 0.0 | 0.009783 | -0.002067 | 0.013717 | 0.000607 | 0.008753 | ... | 0.001314 | 0.010179 | 0.007442 | 0.007351 | 0.006116 | 0.0 | -0.006470 | 0.035676 | 0.007467 | 0.0 |
| 2011-01-12 00:00:00+00:00 | 0.017254 | -0.008237 | 0.013387 | 0.008133 | 0.0 | -0.005979 | -0.001011 | 0.022969 | 0.017950 | 0.000257 | ... | 0.004986 | 0.015666 | 0.011763 | 0.027182 | 0.004386 | 0.0 | 0.002631 | 0.014741 | -0.011903 | 0.0 |
| 2011-01-13 00:00:00+00:00 | -0.004559 | 0.000955 | 0.003031 | 0.003657 | 0.0 | 0.014925 | -0.004451 | -0.000400 | -0.005719 | -0.005012 | ... | 0.030499 | -0.003217 | 0.001694 | 0.000547 | -0.018235 | 0.0 | -0.005084 | -0.004665 | -0.009178 | 0.0 |
5 rows × 490 columns
TODO: Factor Exposures
In the code below, write a function, factor_betas(pca, factor_beta_indices, factor_beta_columns) that calculates the factor exposures from Scikit-Learn's PCA() class. Remember the matrix of factor exposures, $\textbf{B}$, describes the coordintates of the Principal Components in the original basis. The pca parameter must be a Scikit-Learn's pca object, that has fit the model with the returns. In other words, you must first run pca.fit(returns) before passing this parameter into the function. Later in this notebook we will create a function, fit_pca(), that will fit the pca model and return the pcaobject. The factor_beta_indices parameter must be a 1 dimensional ndarray containg the column names of the returns dataframe. The factor_beta_columns parameter must be a 1 dimensional ndarray containing evenly spaced integers from 0 up to the number of principal components you used in your pca model minus one. For example, if you used 5 principal compoenents in your pca model, pca = PCA(n_components = 5), then factor_beta_columns = [0, 1, 2, 3, 4]. This function has to return a Pandas dataframe with the factor exposures, where the factor_beta_indices correspond to the indices of the dataframe and the factor_beta_columns correspond to the column names of the dataframe.
def factor_betas(pca, factor_beta_indices, factor_beta_columns):
#Implement Function
assert len(factor_beta_indices.shape) == 1
assert len(factor_beta_columns.shape) == 1
return pd.DataFrame(pca.components_.T, factor_beta_indices, factor_beta_columns)TODO: Factor Retuns
In the code below, write a function, factor_returns(pca, returns, factor_return_indices, factor_return_columns) that calculates the factor returns from Scikit-Learn's PCA() class. Remember the matrix of factor returns, $\textbf{f}$, represents the returns written in the new basis. The pca parameter must be a Scikit-Learn's pca object, that has fit the model with the returns. In other words, you must first run pca.fit(returns) before passing this parameter into the function. Later in this notebook we will create a function, fit_pca(), that will fit the pca model and return the pcaobject. The returns parameter is the pandas dataframe of returns given at the begining of the notebook. The factor_return_indices parameter must be a 1 dimensional ndarray containing the trading dates (Pandas DatetimeIndex) in the returns dataframe. The factor_return_columns parameter must be a 1 dimensional ndarray containing evenly spaced integers from 0 up to the number of principal components you used in your pca model minus one. For example, if you used 5 principal compoenents in your pca model, pca = PCA(n_components = 5), then factor_beta_columns = [0, 1, 2, 3, 4]. This function has to return a Pandas dataframe with the factor returns, where the factor_return_indices correspond to the indices of the dataframe and the factor_return_columns correspond to the column names of the dataframe.
import pandas as pd
def factor_returns(pca, returns, factor_return_indices, factor_return_columns):
#Implement Function
assert len(factor_return_indices.shape) == 1
assert len(factor_return_columns.shape) == 1
return pd.DataFrame(pca.transform(returns), factor_return_indices, factor_return_columns)TODO: Idiosyncratic Risk Matrix
Let's review how we can calculate the Idiosyncratic Risk Matrix $\textbf{S}$. We know that:
$$
\textbf{s} = \textbf{r} - \textbf{B}\textbf{f}
$$
We refer to $\textbf{s}$ as the residuals. To calculate the idiosyncratic or specific risk matrix $\textbf{S}$, we have to calculate the covariance matrix of the residuals, $\textbf{s}$, and set the off-diagonal elements to zero.
With this in mind, in the code below cerate a function, idiosyncratic_var_matrix(returns, factor_returns, factor_betas, ann_factor) that calclates the annualized Idiosyncratic Risk Matrix. The returns parameter is the pandas dataframe of returns given at the begining of the notebook. The factor_returns parameter is the output of the factor_returns() function created above. Similarly, the factor_betas parameter is the output of the factor_betas() function created above. The ann_factor parameter is an integer representing the annualization factor.
Remember that if the returns time series are daily returns, then when we calculate the Idiosyncratic Risk Matrix we will get values on a daily basis. We can annualize these values simply by multiplying the whole Idiosyncratic Risk Matrix by an annualization factor of 252. Remember we don't need the square root of the factor because our numbers here are variances not standard deviations.
The function must return a pandas dataframe with the annualized Idiosyncratic Risk Matrix containing the covariance of the residuals in its main diagonal and with all the off-diagonal elements set to zero.
def idiosyncratic_var_matrix(returns, factor_returns, factor_betas, ann_factor):
#Implement Function
common_returns_ = pd.DataFrame(np.dot(factor_returns, factor_betas.T), returns.index, returns.columns)
residuals_ = (returns - common_returns_)
return pd.DataFrame(np.diag(np.var(residuals_))*ann_factor, returns.columns, returns.columns)TODO: Factor Covariance Matrix
To calculate the annualized factor covariance matrix, $\textbf{F}$, we use the following equation:
$$
\textbf{F} = \frac{1}{N -1}\textbf{f}\textbf{f}^T
$$
where, $N$ is the number of elements in $\textbf{f}$. Recall that the factor covariance matrix, $\textbf{F}$, is a diagonal matrix.
With this in mind, create a function, factor_cov_matrix(factor_returns, ann_factor) that calculates the annualized factor covariance matrix from the factor returns $\textbf{f}$. The factor_returns parameter is the output of the factor_returns() function created above and the ann_factor parameter is an integer representing the annualization factor. The function must return a diagonal numpy ndarray
HINT : You can calculate the factor covariance matrix $\textbf{F}$ very easily using Numpy's .var method. The $\frac{1}{N -1}$ factor can be taken into account using the ddof keyword.
def factor_cov_matrix(factor_returns, ann_factor):
#Implement Function
return np.diag(factor_returns.var(axis=0, ddof=1)*ann_factor)TODO: Perfom PCA
In the code below, create a function, fit_pca(returns, num_factor_exposures, svd_solver) that uses Scikit-Learn's PCA() class to fit the returns dataframe with the given number of num_factor_exposures (Principal Components) and with the given svd_solver. The returns parameter is the pandas dataframe of returns given at the begining of the notebook. The num_factor_exposures parameter is an integer representing the number of Principal Components you want to use in your PCA algorithm. The svd_solver parameter is a string that determines the type of solver you want to use in your PCA algorithm. To see the type of solvers that you can use, see the Scikit-Learn documentation. The function must fit the returns and return the pca object.
from sklearn.decomposition import PCA
def fit_pca(returns, num_factor_exposures, svd_solver):
#TODO: Implement function
pca = PCA(n_components=num_factor_exposures, svd_solver=svd_solver)
pca.fit(returns)
return pcaTODO: Create The Risk Model
In the code below, create a class:
class RiskModel(object):
def __init__(self, returns, ann_factor, num_factor_exposures, pca):where the returns parameter is the pandas dataframe of returns given at the begining of the notebook. The ann_factor parameter is an integer representing the annualization factor. The num_factor_exposures parameter is an integer representing the number of Principal Components you want to use in your PCA algorithm. The pca parameter is the output of the fit_pca() function created above. The class must contain all the fucntions created above. For example, to include the Factor covariance matrix we will use:
self.factor_cov_matrix_ = factor_cov_matrix(self.factor_returns_, ann_factor)import numpy as np
class RiskModel(object):
def __init__(self, returns, ann_factor, num_factor_exposures, pca):
self.factor_betas_ = factor_betas(pca, returns.columns.values, np.arange(num_factor_exposures))
self.factor_returns_ = factor_returns(pca, returns, returns.index, np.arange(num_factor_exposures))
self.factor_cov_matrix_ = factor_cov_matrix(self.factor_returns_, ann_factor)
self.idiosyncratic_var_matrix_ = idiosyncratic_var_matrix(returns, self.factor_returns_, self.factor_betas_, ann_factor)
# Set the annualized factor
ann_factor = 252
# Set the number of factor exposures (principal components) for the PCA algorithm
num_factor_exposures = 20
# Set the svd solver for the PCA algorithm
svd_solver = 'full'
# Fit the PCA Model using the fit_pca() fucntion
pca = fit_pca(returns, num_factor_exposures, svd_solver)
# Create a RiskModel object
rm = RiskModel(returns, ann_factor, num_factor_exposures, pca)TODO: Print The Factor Exposures
rm.factor_betas_| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equity(0 [A]) | -0.043168 | 0.019551 | -0.009934 | 0.010540 | -0.018198 | 0.010745 | 0.001129 | 0.039739 | -0.013805 | 0.012737 | -0.023840 | -0.001417 | 0.020993 | 0.034610 | -0.030489 | 0.033606 | -0.011429 | -0.011743 | 0.005269 | -0.005353 |
| Equity(1 [AAL]) | -0.058745 | 0.196377 | 0.078688 | 0.082096 | 0.348478 | -0.138082 | 0.071293 | 0.105248 | -0.045890 | -0.085478 | 0.003283 | 0.105343 | 0.067216 | -0.044060 | -0.022316 | 0.017263 | -0.033108 | 0.013981 | -0.046807 | -0.015991 |
| Equity(490 [ZTS]) | -0.013672 | 0.018922 | 0.018679 | -0.048787 | 0.012637 | 0.048319 | -0.002055 | 0.016134 | -0.019190 | -0.030720 | -0.040314 | -0.030853 | -0.056128 | -0.015419 | 0.001082 | -0.023961 | -0.010268 | 0.036824 | 0.008340 | 0.015002 |
490 rows × 20 columns
TODO: Print The Factor Returns
rm.factor_returns_| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011-01-07 00:00:00+00:00 | -0.000574 | -0.030781 | 0.011428 | -0.023880 | 0.074403 | -0.064550 | 0.009386 | -0.032856 | -0.047045 | -0.015925 | 0.006513 | -0.087893 | -0.000682 | 0.007119 | -0.021873 | 0.002709 | 0.012091 | -0.015344 | 0.009317 | -0.036960 |
| 2011-01-10 00:00:00+00:00 | -0.003338 | -0.029503 | 0.063908 | -0.003170 | -0.040026 | -0.062263 | -0.002421 | 0.002570 | 0.039893 | -0.054881 | 0.037833 | 0.042430 | -0.009385 | 0.003108 | -0.031709 | -0.028422 | -0.007200 | 0.029072 | -0.005645 | -0.000275 |
| 2016-01-04 00:00:00+00:00 | 0.304973 | -0.181489 | -0.025222 | 0.002928 | 0.022257 | -0.072114 | 0.011806 | -0.007387 | -0.035864 | -0.040566 | 0.069396 | 0.068978 | -0.028233 | 0.042410 | 0.009863 | -0.002565 | 0.019311 | -0.010162 | 0.000179 | 0.023725 |
1256 rows × 20 columns
TODO: Print The Idiosyncratic Risk Matrix
rm.idiosyncratic_var_matrix_ | Equity(0 [A]) | Equity(1 [AAL]) | Equity(2 [AAP]) | Equity(3 [AAPL]) | Equity(4 [ABBV]) | Equity(5 [ABC]) | Equity(6 [ABT]) | Equity(7 [ACN]) | Equity(8 [ADBE]) | Equity(9 [ADI]) | ... | Equity(481 [XL]) | Equity(482 [XLNX]) | Equity(483 [XOM]) | Equity(484 [XRAY]) | Equity(485 [XRX]) | Equity(486 [XYL]) | Equity(487 [YUM]) | Equity(488 [ZBH]) | Equity(489 [ZION]) | Equity(490 [ZTS]) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equity(0 [A]) | 0.022725 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.00000 | 0.000000 | 0.000000 |
490 rows × 490 columns
TODO: Print The Factor Covariance Matrix
rm.factor_cov_matrix_array([[ 14.01830425, 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 1.10591127, 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0.77099145, 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0.61798821,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0.47589087, 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0.43653315, 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0.3873247 , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.34930223,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0.34350302, 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0.31674219, 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0.28186803, 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.2762745 ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0.26857691, 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0.24981278, 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0.23329965, 0. ,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.21393011,
0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0.20845473, 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0.19480492, 0. , 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0.19126517, 0. ],
[ 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.18725609]])View The Percent of Variance Explained by Each Factor
%matplotlib inline
import matplotlib.pyplot as plt
# Set the default figure size
plt.rcParams['figure.figsize'] = [10.0, 6.0]
# Make the bar plot
plt.bar(np.arange(num_factor_exposures), pca.explained_variance_ratio_);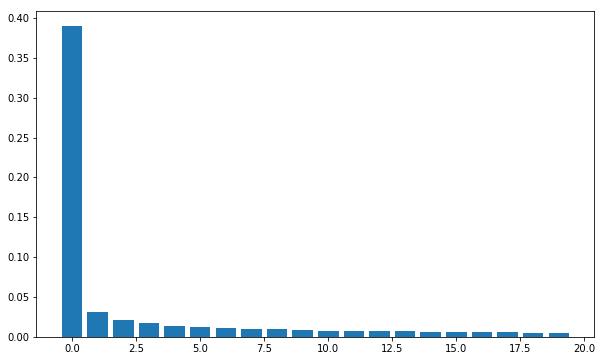
You can see that the first factor dominates. The precise defintion of each factor in a latent model is unknown, however we can guess at the likely intepretation.
View The Factor Returns
Remember that the factors returns don't necessarily have direct interpretations in the real world but you can thinik of them as returns time series for some kind of latent or unknown driver of return variance.
%matplotlib inline
import matplotlib.pyplot as plt
# Set the default figure size
plt.rcParams['figure.figsize'] = [10.0, 6.0]
rm.factor_returns_.loc[:,0:5].cumsum().plot();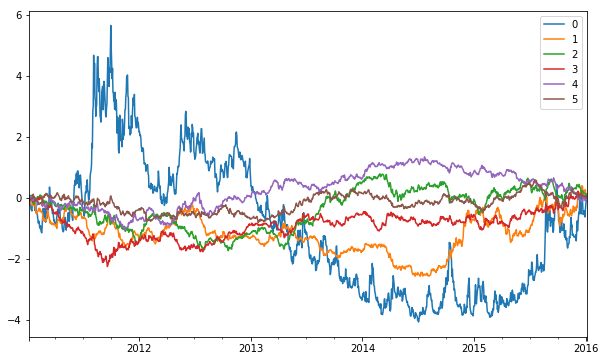
为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



