AI For Trading:Ranked information Coefficient (Rank IC) (69)
RankIC,即某时点某因子在全部股票因子暴露值排名与其下期回报排名的截面相关系数。不同信息系数的计算是有差异的,目前较常用的是Rank IC。
Rank IC
A useful evaluation metric is the rank information coefficient, often referred to as rank IC.
The rank IC tells us whether the ranks of our alpha values are correlated with the ranks of the future returns.
In other words, if the alpha factor suggested that we bet more on stock ABC and less on stock XYZ, was the future return of ABC relatively high? Was a future return of stock XYZ relatively low? If the future performance of the assets matched the expectations that was suggested by the alpha factor, then the information coefficient would be higher.
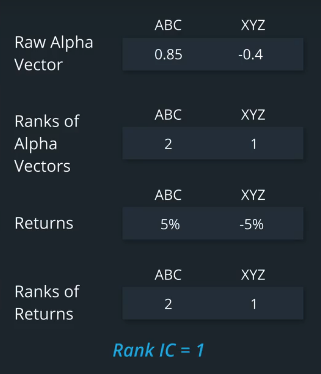
Otherwise, it would be lower and possibly negative.For some insight, let's first look at this without ranking.Let's pretend there are just two stocks in our universe, ABC and XYZ. Stock ABC has a high positive alpha value and
XYZ has a very negative alpha value as calculated before time,t. Between time T to time T plus one,the return of stock ABC is positive and XYZ's return is negative.
These alpha values appear to be correlated with the forward asset returns. Note here, when we say asset return,
we're referring to the return of each stock for each time period. We also specify that the asset return is a forward return.
We say, forward asset return to specify that the return is in the future or forward in time compared to when the alpha value was calculated. So, if the alpha values are calculated before time t, then the forward asset return is calculated with data that occurs later from time t to time t plus one. To make our evaluation more robust, we want to use ranks instead of the original alpha values and returns.
Stock ABC is alpha value before time t is high and positive, while stock XYZ is alpha value, is negative. So, ABC has a higher rank of two and XYZ has a lower rank of one.
The forward asset return of ABC from time t to time t plus one is higher compared to XYZ. So, the rank of ABC's forward asset return is two, and the rank of XYZ's forward asset return is one.
If the ranks of the alpha values and the ranks of the forward asset returns are highly correlated, the rank IC metric would be close to one.
In this example, since the ranks of the two alpha values are equal to the ranks of the two forward asset returns, then the rank IC in this example is one.
Spearman rank correlation and Pearson correlation
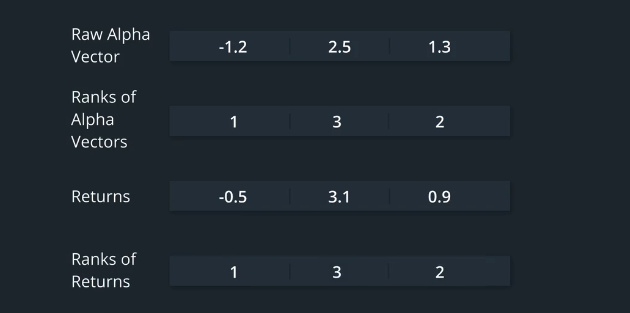
More formally, here are the steps we'll take to calculate the Rank IC.For each time period,rank the raw Alpha factor.
For instance, with a stock universe of three stocks, the lowest Alpha value has a rank of 1,and the highest Alpha value has a rank of 3.Also, calculate the forward asset returns and rank them.The stock with the lowest forward return has a rank of 1,and the stock with the highest forward return has a rank of 3.
The correlation of ranked values is called the Spearman rank correlation to distinguish it from the Pearson correlation.
Let's clarify these two terms.
The Pearson correlation is what you're probably familiar with, is the covariance of two variables which is then
re-scaled using the standard deviations of the two variables. The denominator makes the correlation range from negative 1 to 1.
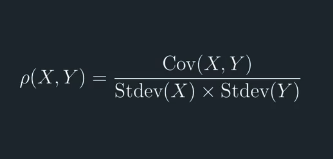
The Pearson Correlation is also the square root of the R-squared in a linear regression. Recall that the R-squared represents the proportion of variance in one variable that is explained by the second variable.
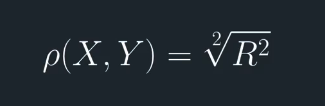
The Spearman rank correlation is the same as the Pearson correlation, except the variables x and y are converted to ranks before calculating the covariance and standard deviations.
To get the rank IC, calculate the correlation between the ranked Alpha vector and the ranked forward asset returns for a single time period. Repeat this over multiple time periods to get a time series.
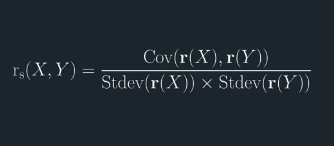
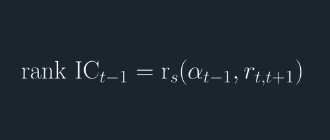
You may be wondering why we use the Spearman rank correlation as opposed to the Pearson correlation.That is why do we use ranking?
The answer is because we don't care about being wrong in the right direction.Let's say stock ABC is our top Alpha value in a universe of 2,000 stocks.
Our alpha value will likely be a small positive value, then imagine that ABC outperforms all the other stocks not by a small amount, but by a very large amount.
The Pearson correlation would calculate a lower score effectively penalizing us because we didn't get the relative magnitude correct.
On the other hand, the Spearman rank correlation would not be affected by this. We prefer to use ranking to evaluate our performance because what matters is that our Alpha is still profitable as we had hoped.
练习题
The documentation for : factor_infomation_coefficient is here
Looking at the source code, can you see what scipy function is called in order to calculate the rank IC?

Ranked Information Coefficient Exercise
Install packages
import sys!{sys.executable} -m pip install -r requirements.txtimport cvxpy as cvx
import numpy as np
import pandas as pd
import time
import os
import quiz_helper
import matplotlib.pyplot as plt%matplotlib inline
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (14, 8)data bundle
import os
import quiz_helper
from zipline.data import bundlesos.environ['ZIPLINE_ROOT'] = os.path.join(os.getcwd(), '..', '..','data','module_4_quizzes_eod')
ingest_func = bundles.csvdir.csvdir_equities(['daily'], quiz_helper.EOD_BUNDLE_NAME)
bundles.register(quiz_helper.EOD_BUNDLE_NAME, ingest_func)
print('Data Registered')Build pipeline engine
from zipline.pipeline import Pipeline
from zipline.pipeline.factors import AverageDollarVolume
from zipline.utils.calendars import get_calendar
universe = AverageDollarVolume(window_length=120).top(500)
trading_calendar = get_calendar('NYSE')
bundle_data = bundles.load(quiz_helper.EOD_BUNDLE_NAME)
engine = quiz_helper.build_pipeline_engine(bundle_data, trading_calendar)View Data露
With the pipeline engine built, let's get the stocks at the end of the period in the universe we're using. We'll use these tickers to generate the returns data for the our risk model.
universe_end_date = pd.Timestamp('2016-01-05', tz='UTC')
universe_tickers = engine\
.run_pipeline(
Pipeline(screen=universe),
universe_end_date,
universe_end_date)\
.index.get_level_values(1)\
.values.tolist()
universe_tickersGet Returns data
from zipline.data.data_portal import DataPortal
data_portal = DataPortal(
bundle_data.asset_finder,
trading_calendar=trading_calendar,
first_trading_day=bundle_data.equity_daily_bar_reader.first_trading_day,
equity_minute_reader=None,
equity_daily_reader=bundle_data.equity_daily_bar_reader,
adjustment_reader=bundle_data.adjustment_reader)Get pricing data helper function
def get_pricing(data_portal, trading_calendar, assets, start_date, end_date, field='close'):
end_dt = pd.Timestamp(end_date.strftime('%Y-%m-%d'), tz='UTC', offset='C')
start_dt = pd.Timestamp(start_date.strftime('%Y-%m-%d'), tz='UTC', offset='C')
end_loc = trading_calendar.closes.index.get_loc(end_dt)
start_loc = trading_calendar.closes.index.get_loc(start_dt)
return data_portal.get_history_window(
assets=assets,
end_dt=end_dt,
bar_count=end_loc - start_loc,
frequency='1d',
field=field,
data_frequency='daily')get pricing data into a dataframe
returns_df = \
get_pricing(
data_portal,
trading_calendar,
universe_tickers,
universe_end_date - pd.DateOffset(years=5),
universe_end_date)\
.pct_change()[1:].fillna(0) #convert prices into returns
returns_dfSector data helper function
We'll create an object for you, which defines a sector for each stock. The sectors are represented by integers. We inherit from the Classifier class. Documentation for Classifier, and the source code for Classifier
from zipline.pipeline.classifiers import Classifier
from zipline.utils.numpy_utils import int64_dtype
class Sector(Classifier):
dtype = int64_dtype
window_length = 0
inputs = ()
missing_value = -1
def __init__(self):
self.data = np.load('../../data/project_4_sector/data.npy')
def _compute(self, arrays, dates, assets, mask):
return np.where(
mask,
self.data[assets],
self.missing_value,
)sector = Sector()We'll use 2 years of data to calculate the factor
Note: Going back 2 years falls on a day when the market is closed. Pipeline package doesn't handle start or end dates that don't fall on days when the market is open. To fix this, we went back 2 extra days to fall on the next day when the market is open.
factor_start_date = universe_end_date - pd.DateOffset(years=2, days=2)
factor_start_dateCreate smoothed momentum factor
from zipline.pipeline.factors import Returns
from zipline.pipeline.factors import SimpleMovingAverage
# create a pipeline called p
p = Pipeline(screen=universe)
# create a factor of one year returns, deman by sector, then rank
factor = (
Returns(window_length=252, mask=universe).
demean(groupby=Sector()). #we use the custom Sector class that we reviewed earlier
rank().
zscore()
)
# Use this factor as input into SimpleMovingAverage, with a window length of 5
# Also rank and zscore (don't need to de-mean by sector, s)
factor_smoothed = (
SimpleMovingAverage(inputs=[factor], window_length=5).
rank().
zscore()
)
# add the unsmoothed factor to the pipeline
p.add(factor, 'Momentum_Factor')
# add the smoothed factor to the pipeline too
p.add(factor_smoothed, 'Smoothed_Momentum_Factor')visualize the pipeline
Note that if the image is difficult to read in the notebook, right-click and view the image in a separate tab.
p.show_graph(format='png')run pipeline and view the factor data
df = engine.run_pipeline(p, factor_start_date, universe_end_date)df.head()Evaluate Factors
We'll go over some tools that we can use to evaluate alpha factors. To do so, we'll use the alphalens library
Import alphalens
import alphalens as alGet price data
Note, we already got the price data and converted it to returns, which we used to calculate a factor. We'll retrieve the price data again, but won't convert these to returns. This is because we'll use alphalens functions that take their input as prices and not returns.
Define the list of assets
Just to make sure we get the prices for the stocks that have factor values, we'll get the list of assets, which may be a subset of the original universe
# get list of stocks in our portfolio (tickers that identify each stock)
assets = df.index.levels[1].values.tolist()
print(f"stock universe number of stocks {len(universe_tickers)}, and number of stocks for which we have factor values {len(assets)}")factor_start_datepricing = get_pricing(
data_portal,
trading_calendar,
assets, #notice that we used assets instead of universe_tickers; in this example, they're the same
factor_start_date, # notice we're using the same start and end dates for when we calculated the factor
universe_end_date)Double check the dates of the pricing data
Check that they make sense compared to the factor data
pricing.head(2)pricing.tail(2)pricing.shapeCompare to the factor data for a single stock
stock_index_name = df.index.get_level_values(1)[3] #just pick a stock; in this case, stock number 3 is AAPL
single_stock_factor_df = df[np.in1d(df.index.get_level_values(1), [stock_index_name])]single_stock_factor_df.head(2)single_stock_factor_df.tail(2)single_stock_factor_df.shapePrepare data for use in alphalens
factor_names = df.columns
print(f"The factor names are {factor_names}")
# Use a dictionary to store each dataframe, one for each factor and its associated forward returns
factor_data = {}
for factor_name in factor_names:
print("Formatting factor data for: " + factor_name)
# Get clean factor and forward returns for each factor
# Choose single period returns (daily returns)
factor_data[factor_name] = al.utils.get_clean_factor_and_forward_returns(
factor=df[factor_name],
prices=pricing,
periods=[1])Rank IC
The factor_information_coefficient function in alphalens documentation is here.
Also pasted below:
Computes the Spearman Rank Correlation based Information Coefficient (IC) between factor values and N period forward returns for each period in the factor index.
Parameters:
factor_data : pd.DataFrame - MultiIndex
A MultiIndex DataFrame indexed by date (level 0) and asset (level 1), containing the values for a single alpha factor, forward returns for each period, the factor quantile/bin that factor value belongs to, and (optionally) the group the asset belongs to. - See full explanation in utils.get_clean_factor_and_forward_returns
group_adjust : bool
Demean forward returns by group before computing IC.
by_group : bool
If True, compute period wise IC separately for each group.
Returns:
ic : pd.DataFrame
Spearman Rank correlation between factor and provided forward returns.Quiz 1
Use alphalens to calculate the rank IC for each factor
Answer 1
ls_rank_ic = []
for i, factor_name in enumerate(factor_names):
#TODO: use alphalens function "factor_information_coefficient" to calculate rank IC
rank_ic = al.performance.factor_information_coefficient(factor_data[factor_name])
rank_ic.columns = [factor_name]
ls_rank_ic.append(rank_ic)View rank IC
ls_rank_ic[0]['Momentum_Factor'].plot(title="rank IC")
ls_rank_ic[1]['Smoothed_Momentum_Factor'].plot(style='--')Quiz 2
What does it mean when the rank IC value is above the zero line?
Answer 2
The rank IC is above zero when the correlation between the factor values and the forward returns is positive (we ideally want to find factors for which the rank IC is more positive).
为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



