AI For Trading: Introduction to Neural Networks (95)
关于神经网络的知识,我们在基础课已经学过了,这里只做一个简单的回顾。
Notebook: Gradient Descent
Implementing the Gradient Descent Algorithm
In this lab, we'll implement the basic functions of the Gradient Descent algorithm to find the boundary in a small dataset. First, we'll start with some functions that will help us plot and visualize the data.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
#Some helper functions for plotting and drawing lines
def plot_points(X, y):
admitted = X[np.argwhere(y==1)]
rejected = X[np.argwhere(y==0)]
plt.scatter([s[0][0] for s in rejected], [s[0][1] for s in rejected], s = 25, color = 'blue', edgecolor = 'k')
plt.scatter([s[0][0] for s in admitted], [s[0][1] for s in admitted], s = 25, color = 'red', edgecolor = 'k')
def display(m, b, color='g--'):
plt.xlim(-0.05,1.05)
plt.ylim(-0.05,1.05)
x = np.arange(-10, 10, 0.1)
plt.plot(x, m*x+b, color)Reading and plotting the data
data = pd.read_csv('data.csv', header=None)
X = np.array(data[[0,1]])
y = np.array(data[2])
plot_points(X,y)
plt.show()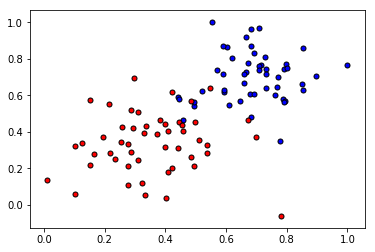
TODO: Implementing the basic functions
Here is your turn to shine. Implement the following formulas, as explained in the text.
- Sigmoid activation function
$$\sigma(x) = \frac{1}{1+e^{-x}}$$
- Output (prediction) formula
$$\hat{y} = \sigma(w_1 x_1 + w_2 x_2 + b)$$
- Error function
$$Error(y, \hat{y}) = - y \log(\hat{y}) - (1-y) \log(1-\hat{y})$$
- The function that updates the weights
$$ w_i \longrightarrow w_i + \alpha (y - \hat{y}) x_i$$
$$ b \longrightarrow b + \alpha (y - \hat{y})$$
# Implement the following functions
# Activation (sigmoid) function
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def output_formula(features, weights, bias):
return sigmoid(np.dot(features, weights) + bias)
def error_formula(y, output):
return - y*np.log(output) - (1 - y) * np.log(1-output)
def update_weights(x, y, weights, bias, learnrate):
output = output_formula(x, weights, bias)
d_error = y - output
weights += learnrate * d_error * x
bias += learnrate * d_error
return weights, biasTraining function
This function will help us iterate the gradient descent algorithm through all the data, for a number of epochs. It will also plot the data, and some of the boundary lines obtained as we run the algorithm.
np.random.seed(44)
epochs = 100
learnrate = 0.01
def train(features, targets, epochs, learnrate, graph_lines=False):
errors = []
n_records, n_features = features.shape
last_loss = None
weights = np.random.normal(scale=1 / n_features**.5, size=n_features)
bias = 0
for e in range(epochs):
del_w = np.zeros(weights.shape)
for x, y in zip(features, targets):
output = output_formula(x, weights, bias)
error = error_formula(y, output)
weights, bias = update_weights(x, y, weights, bias, learnrate)
# Printing out the log-loss error on the training set
out = output_formula(features, weights, bias)
loss = np.mean(error_formula(targets, out))
errors.append(loss)
if e % (epochs / 10) == 0:
print("\n========== Epoch", e,"==========")
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
predictions = out > 0.5
accuracy = np.mean(predictions == targets)
print("Accuracy: ", accuracy)
if graph_lines and e % (epochs / 100) == 0:
display(-weights[0]/weights[1], -bias/weights[1])
# Plotting the solution boundary
plt.title("Solution boundary")
display(-weights[0]/weights[1], -bias/weights[1], 'black')
# Plotting the data
plot_points(features, targets)
plt.show()
# Plotting the error
plt.title("Error Plot")
plt.xlabel('Number of epochs')
plt.ylabel('Error')
plt.plot(errors)
plt.show()Time to train the algorithm!
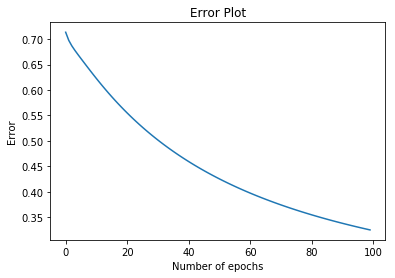
When we run the function, we'll obtain the following:
- 10 updates with the current training loss and accuracy
- A plot of the data and some of the boundary lines obtained. The final one is in black. Notice how the lines get closer and closer to the best fit, as we go through more epochs.
- A plot of the error function. Notice how it decreases as we go through more epochs.
train(X, y, epochs, learnrate, True)========== Epoch 0 ==========
Train loss: 0.713584519538
Accuracy: 0.4
========== Epoch 10 ==========
Train loss: 0.622583521045
Accuracy: 0.59
========== Epoch 20 ==========
Train loss: 0.554874408367
Accuracy: 0.74
========== Epoch 30 ==========
Train loss: 0.501606141872
Accuracy: 0.84
========== Epoch 40 ==========
Train loss: 0.459333464186
Accuracy: 0.86
========== Epoch 50 ==========
Train loss: 0.425255434335
Accuracy: 0.93
========== Epoch 60 ==========
Train loss: 0.397346157167
Accuracy: 0.93
========== Epoch 70 ==========
Train loss: 0.374146976524
Accuracy: 0.93
========== Epoch 80 ==========
Train loss: 0.354599733682
Accuracy: 0.94
========== Epoch 90 ==========
Train loss: 0.337927365888
Accuracy: 0.94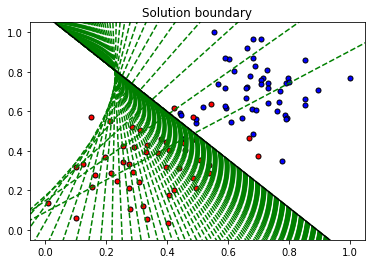
为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



