AI For Trading: Word Embeddings (99)
Word Embeddings
这篇博文,我们将讨论如何使用神经网络处理自然语言,及论词嵌入。
词嵌入是指模型学习将词汇表中的一组字词或短语映射到数字向量,这些向量称为嵌入。我们可以使用神经网络学习构建词嵌入,通常,这种技巧可以降低文本数据的维数,但是这些嵌入模型也能够学习,关于词汇表中字词的有趣特性,我们将重点讲解 Word2Vec 嵌入模型 ,它会学习将字词映射到包含语义的嵌入,例如,嵌入可以学习当前的时态动词,与过去时态的关系。
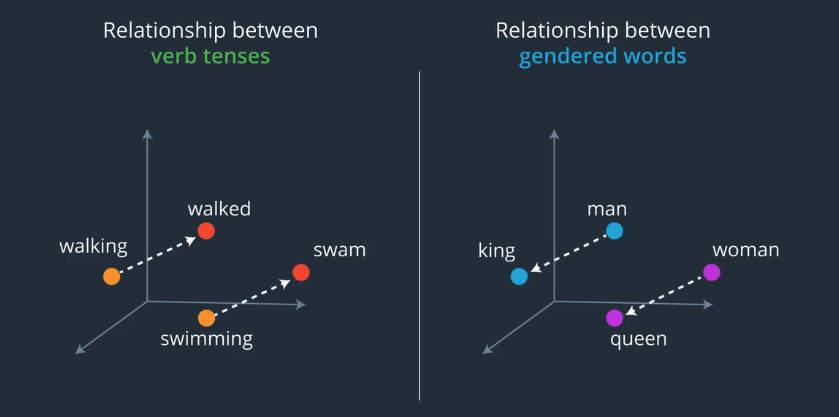
你可以将这些嵌入看做一种向量,这些向量学会从数学角度表示词汇表中字词之间的关系,注意,嵌入式genuine一段文本学习而来的,因此源文本里的任何字词关系将体现到嵌入里。如果文本包含错误信息或性别偏见关系,这些特性将提现在嵌入里,实际上词嵌入消除偏见,是一个很活跃的研究领域,我们先讨论词嵌入的基础理论,
Skip-gram Word2Vec
In this notebook, I'll lead you through using PyTorch to implement the Word2Vec algorithm using the skip-gram architecture. By implementing this, you'll learn about embedding words for use in natural language processing. This will come in handy when dealing with things like machine translation.
Readings
Here are the resources I used to build this notebook. I suggest reading these either beforehand or while you're working on this material.
- A really good conceptual overview of Word2Vec from Chris McCormick
- First Word2Vec paper from Mikolov et al.
- Neural Information Processing Systems, paper with improvements for Word2Vec also from Mikolov et al.
Word embeddings
When you're dealing with words in text, you end up with tens of thousands of word classes to analyze; one for each word in a vocabulary. Trying to one-hot encode these words is massively inefficient because most values in a one-hot vector will be set to zero. So, the matrix multiplication that happens in between a one-hot input vector and a first, hidden layer will result in mostly zero-valued hidden outputs.
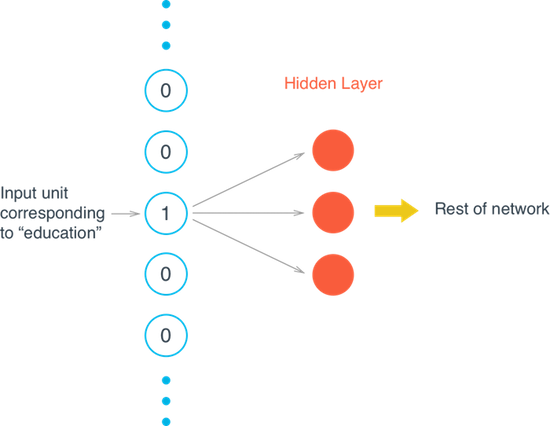
To solve this problem and greatly increase the efficiency of our networks, we use what are called embeddings. Embeddings are just a fully connected layer like you've seen before. We call this layer the embedding layer and the weights are embedding weights. We skip the multiplication into the embedding layer by instead directly grabbing the hidden layer values from the weight matrix. We can do this because the multiplication of a one-hot encoded vector with a matrix returns the row of the matrix corresponding the index of the "on" input unit.

Instead of doing the matrix multiplication, we use the weight matrix as a lookup table. We encode the words as integers, for example "heart" is encoded as 958, "mind" as 18094. Then to get hidden layer values for "heart", you just take the 958th row of the embedding matrix. This process is called an embedding lookup and the number of hidden units is the embedding dimension.
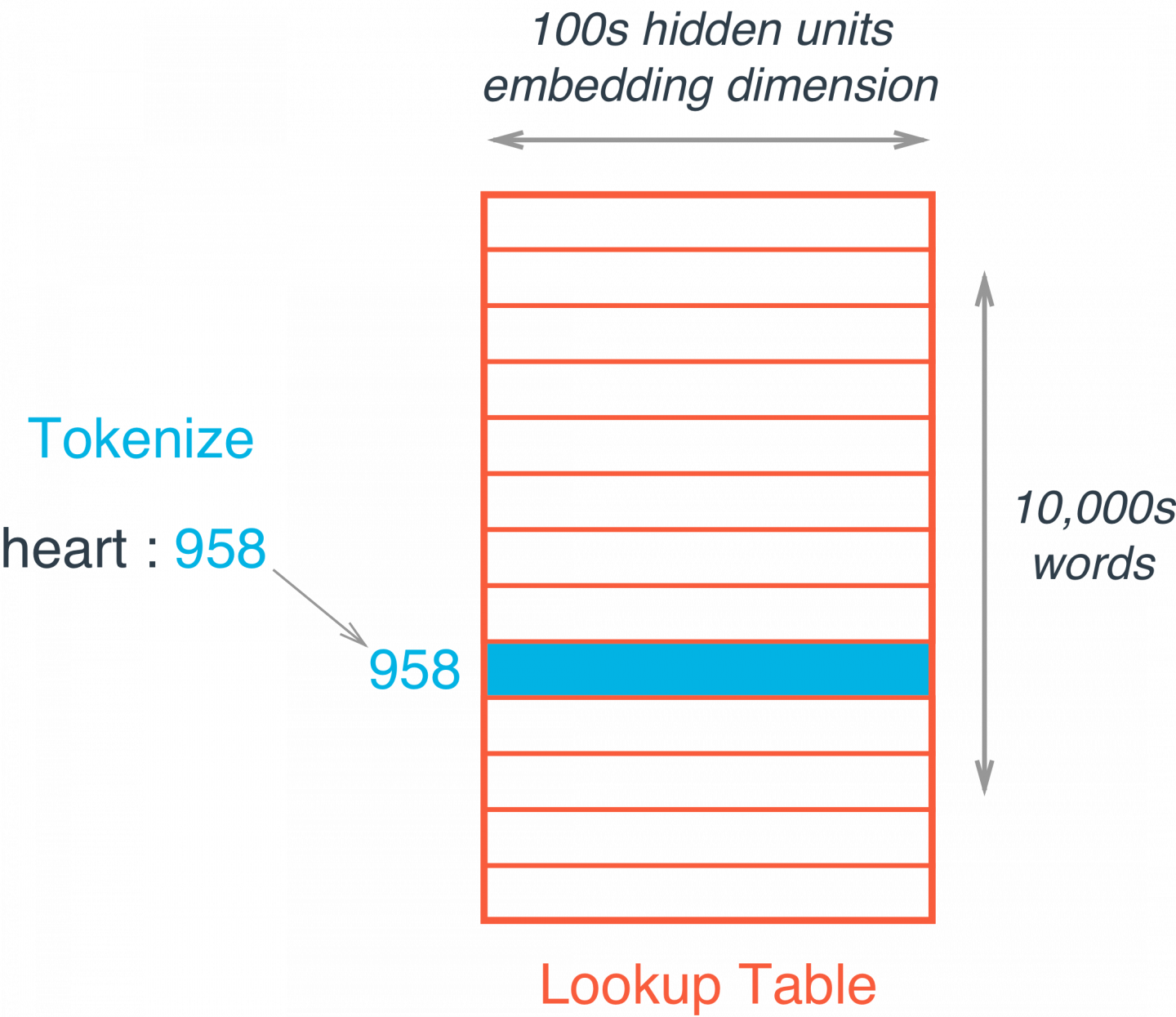
There is nothing magical going on here. The embedding lookup table is just a weight matrix. The embedding layer is just a hidden layer. The lookup is just a shortcut for the matrix multiplication. The lookup table is trained just like any weight matrix.
Embeddings aren't only used for words of course. You can use them for any model where you have a massive number of classes. A particular type of model called Word2Vec uses the embedding layer to find vector representations of words that contain semantic meaning.
Word2Vec
The Word2Vec algorithm finds much more efficient representations by finding vectors that represent the words. These vectors also contain semantic information about the words.

Words that show up in similar contexts, such as "coffee", "tea", and "water" will have vectors near each other. Different words will be further away from one another, and relationships can be represented by distance in vector space.

There are two architectures for implementing Word2Vec:
- CBOW (Continuous Bag-Of-Words) and
- Skip-gram

In this implementation, we'll be using the skip-gram architecture because it performs better than CBOW. Here, we pass in a word and try to predict the words surrounding it in the text. In this way, we can train the network to learn representations for words that show up in similar contexts.
Loading Data
Next, we'll ask you to load in data and place it in the data directory
- Load the text8 dataset; a file of cleaned up Wikipedia article text from Matt Mahoney.
- Place that data in the
datafolder in the home directory. - Then you can extract it and delete the archive, zip file to save storage space.
After following these steps, you should have one file in your data directory: data/text8.
# read in the extracted text file
with open('data/text8') as f:
text = f.read()
# print out the first 100 characters
print(text[:100]) anarchism originated as a term of abuse first used against early working class radicals including tPre-processing
Here I'm fixing up the text to make training easier. This comes from the utils.py file. The preprocess function does a few things:
- It converts any punctuation into tokens, so a period is changed to
<PERIOD>. In this data set, there aren't any periods, but it will help in other NLP problems.- It removes all words that show up five or fewer times in the dataset. This will greatly reduce issues due to noise in the data and improve the quality of the vector representations.
- It returns a list of words in the text.
This may take a few seconds to run, since our text file is quite large. If you want to write your own functions for this stuff, go for it!
import utils
# get list of words
words = utils.preprocess(text)
print(words[:30])['anarchism', 'originated', 'as', 'a', 'term', 'of', 'abuse', 'first', 'used', 'against', 'early', 'working', 'class', 'radicals', 'including', 'the', 'diggers', 'of', 'the', 'english', 'revolution', 'and', 'the', 'sans', 'culottes', 'of', 'the', 'french', 'revolution', 'whilst']# print some stats about this word data
print("Total words in text: {}".format(len(words)))
print("Unique words: {}".format(len(set(words)))) # `set` removes any duplicate words -> 去重Total words in text: 16680599
Unique words: 63641Dictionaries
Next, I'm creating two dictionaries to convert words to integers and back again (integers to words). This is again done with a function in the utils.py file. create_lookup_tables takes in a list of words in a text and returns two dictionaries.
- The integers are assigned in descending frequency order, so the most frequent word ("the") is given the integer 0 and the next most frequent is 1, and so on.
Once we have our dictionaries, the words are converted to integers and stored in the list int_words.
vocab_to_int, int_to_vocab = utils.create_lookup_tables(words)
# 打印
for item in vocab_to_int.items():
print(item)
break
# 从字典中取出数组
int_words = [vocab_to_int[word] for word in words]
print(int_words[:30])('the', 0)
[5233, 3080, 11, 5, 194, 1, 3133, 45, 58, 155, 127, 741, 476, 10571, 133, 0, 27349, 1, 0, 102, 854, 2, 0, 15067, 58112, 1, 0, 150, 854, 3580]Subsampling(二次抽样)
Words that show up often such as "the", "of", and "for" don't provide much context to the nearby words. If we discard some of them, we can remove some of the noise from our data and in return get faster training and better representations. This process is called subsampling by Mikolov. For each word $w_i$ in the training set, we'll discard it with probability given by
$$ P(w_i) = 1 - \sqrt{\frac{t}{f(w_i)}} $$
where $t$ is a threshold parameter and $f(w_i)$ is the frequency of word $w_i$ in the total dataset.
$$ P(0) = 1 - \sqrt{\frac{110^{-5}}{110^6/16*10^6}} = 0.98735 $$
I'm going to leave this up to you as an exercise. Check out my solution to see how I did it.
二次抽样:某些字词几乎永远不会相关,因为它们太常见了,这些字词出现的频率非常高,例如:"the", "of", "for", 等单词,它们不能提供上下文信息,如果丢弃这些常见的字词,就能消除字词数据中的噪点,并且提高训练速度和改善向量表示法的质量,这个流程称为二次抽样。
二次抽样原理:对于训练集中的所有Wi,我们将根据公式计算出其丢弃概率,然后做出丢弃的决定。
Exercise: Implement subsampling for the words in
int_words. That is, go throughint_wordsand discard each word given the probablility $P(w_i)$ shown above. Note that $P(w_i)$ is the probability that a word is discarded. Assign the subsampled data totrain_words.
from collections import Counter
import random
import numpy as np
threshold = 1e-5
word_counts = Counter(int_words)
print(list(word_counts.items())[0]) # dictionary of int_words, how many times they appear
total_count = len(int_words)
freqs = {word: count/total_count for word, count in word_counts.items()}
p_drop = {word: 1 - np.sqrt(threshold/freqs[word]) for word in word_counts}
# discard some frequent words, according to the subsampling equation
# create a new list of words for training
train_words = [word for word in int_words if random.random() < (1 - p_drop[word])]
print(train_words[:30])
#print(train_words[:30])(5233, 303)
[5233, 3133, 10571, 27349, 15067, 58112, 3580, 10712, 19, 362, 3672, 708, 40, 1423, 2757, 567, 686, 7088, 247, 5233, 1052, 44611, 2877, 5233, 11, 5, 200, 602, 2621, 8983]Making batches
Now that our data is in good shape, we need to get it into the proper form to pass it into our network. With the skip-gram architecture, for each word in the text, we want to define a surrounding context and grab all the words in a window around that word, with size $C$.
From Mikolov et al.:
"Since the more distant words are usually less related to the current word than those close to it, we give less weight to the distant words by sampling less from those words in our training examples... If we choose $C = 5$, for each training word we will select randomly a number $R$ in range $[ 1: C ]$, and then use $R$ words from history and $R$ words from the future of the current word as correct labels."
Exercise: Implement a function
get_targetthat receives a list of words, an index, and a window size, then returns a list of words in the window around the index. Make sure to use the algorithm described above, where you chose a random number of words to from the window.
Say, we have an input and we're interested in the idx=2 token, 741:
[5233, 58, 741, 10571, 27349, 0, 15067, 58112, 3580, 58, 10712]For R=2, get_target should return a list of four values:
[5233, 58, 10571, 27349]def get_target(words, idx, window_size=5):
''' Get a list of words in a window around an index. '''
# implement this function
R = np.random.randint(1, window_size+1)
start = idx - R if (idx - R) > 0 else 0
stop = idx + R
target_words = words[start:idx] + words[idx+1:stop+1]
return list(target_words)# test your code!
# run this cell multiple times to check for random window selection
int_text = [i for i in range(10)]
print('Input: ', int_text)
idx=5 # word index of interest
target = get_target(int_text, idx=idx, window_size=5)
print('Target: ', target) # you should get some indices around the idxInput: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Target: [2, 3, 4, 6, 7, 8]Generating Batches
Here's a generator function that returns batches of input and target data for our model, using the get_target function from above. The idea is that it grabs batch_size words from a words list. Then for each of those batches, it gets the target words in a window.
def get_batches(words, batch_size, window_size=5):
''' Create a generator of word batches as a tuple (inputs, targets) '''
#表示获取整数并向下取整
n_batches = len(words)//batch_size
# only full batches
words = words[:n_batches*batch_size]
for idx in range(0, len(words), batch_size):
x, y = [], []
batch = words[idx:idx+batch_size]
for ii in range(len(batch)):
batch_x = batch[ii]
batch_y = get_target(batch, ii, window_size)
y.extend(batch_y)
x.extend([batch_x]*len(batch_y))
yield x, y
int_text = [i for i in range(20)]
x,y = next(get_batches(int_text, batch_size=4, window_size=5))
print('x\n', x)
print('y\n', y)x
[0, 1, 1, 1, 2, 2, 2, 3]
y
[1, 0, 2, 3, 0, 1, 3, 2]Building the graph
Below is an approximate diagram of the general structure of our network.
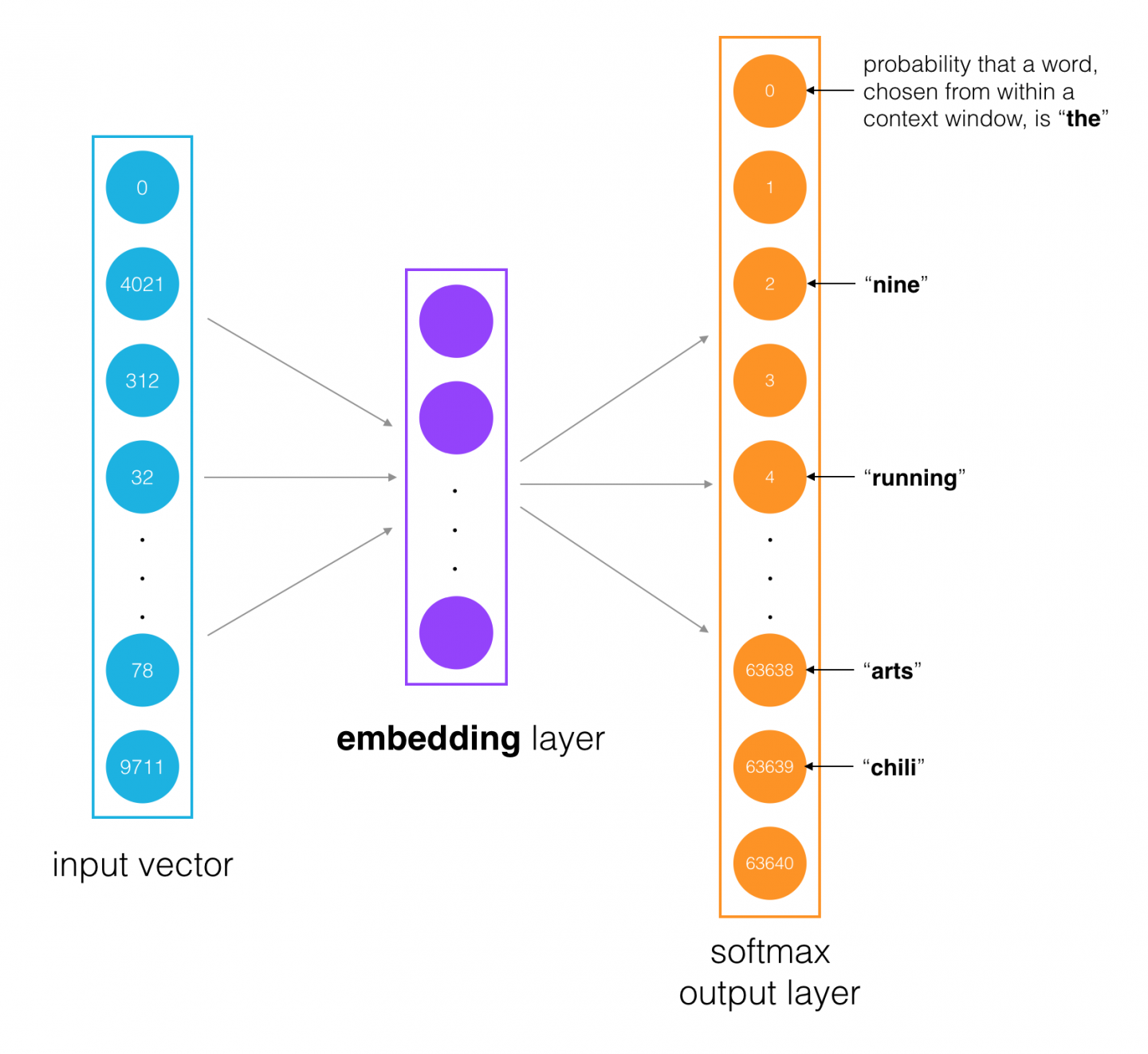
- The input words are passed in as batches of input word tokens.
- This will go into a hidden layer of linear units (our embedding layer).
- Then, finally into a softmax output layer.
We'll use the softmax layer to make a prediction about the context words by sampling, as usual.
The idea here is to train the embedding layer weight matrix to find efficient representations for our words. We can discard the softmax layer because we don't really care about making predictions with this network. We just want the embedding matrix so we can use it in other networks we build using this dataset.
Validation
Here, I'm creating a function that will help us observe our model as it learns. We're going to choose a few common words and few uncommon words. Then, we'll print out the closest words to them using the cosine similarity:
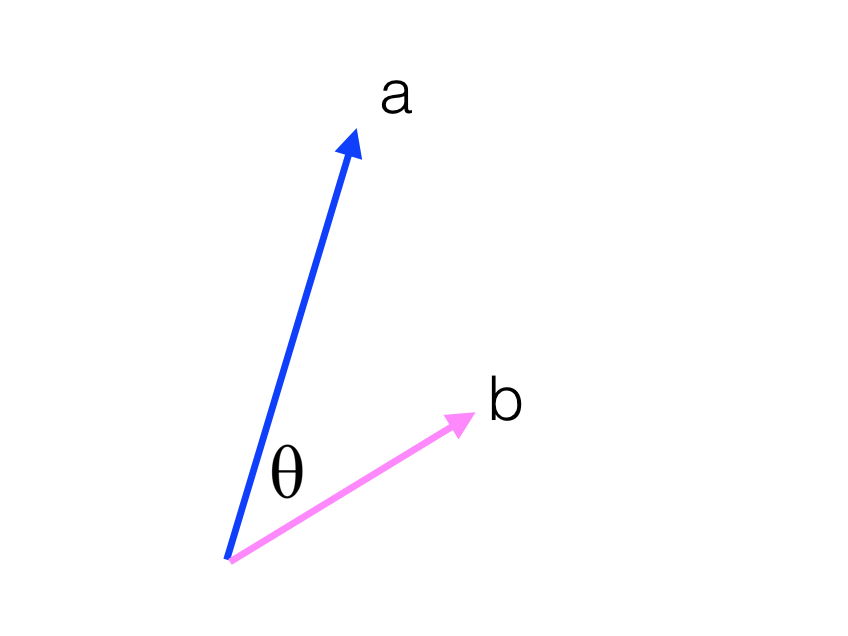
$$
\mathrm{similarity} = \cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}
$$
We can encode the validation words as vectors $\vec{a}$ using the embedding table, then calculate the similarity with each word vector $\vec{b}$ in the embedding table. With the similarities, we can print out the validation words and words in our embedding table semantically similar to those words. It's a nice way to check that our embedding table is grouping together words with similar semantic meanings.
def cosine_similarity(embedding, valid_size=16, valid_window=100, device='cpu'):
""" Returns the cosine similarity of validation words with words in the embedding matrix.
Here, embedding should be a PyTorch embedding module.
"""
# Here we're calculating the cosine similarity between some random words and
# our embedding vectors. With the similarities, we can look at what words are
# close to our random words.
# sim = (a . b) / |a||b|
embed_vectors = embedding.weight
# magnitude of embedding vectors, |b|
magnitudes = embed_vectors.pow(2).sum(dim=1).sqrt().unsqueeze(0)
# pick N words from our ranges (0,window) and (1000,1000+window). lower id implies more frequent
valid_examples = np.array(random.sample(range(valid_window), valid_size//2))
valid_examples = np.append(valid_examples,
random.sample(range(1000,1000+valid_window), valid_size//2))
valid_examples = torch.LongTensor(valid_examples).to(device)
valid_vectors = embedding(valid_examples)
similarities = torch.mm(valid_vectors, embed_vectors.t())/magnitudes
return valid_examples, similaritiesSkipGram model
Define and train the SkipGram model.
You'll need to define an embedding layer and a final, softmax output layer.
An Embedding layer takes in a number of inputs, importantly:
- num_embeddings – the size of the dictionary of embeddings, or how many rows you'll want in the embedding weight matrix
- embedding_dim – the size of each embedding vector; the embedding dimension
import torch
from torch import nn
import torch.optim as optimclass SkipGram(nn.Module):
def __init__(self, n_vocab, n_embed):
super().__init__()
# complete this SkipGram model
self.embed = nn.Embedding(n_vocab, n_embed)
self.output = nn.Linear(n_embed, n_vocab)
self.log_softmax = nn.LogSoftmax(dim=1)
def forward(self, x):
# define the forward behavior
x = self.embed(x)
scores = self.output(x)
log_ps = self.log_softmax(scores)
return log_psTraining
Below is our training loop, and I recommend that you train on GPU, if available.
Note that, because we applied a softmax function to our model output, we are using NLLLoss as opposed to cross entropy. This is because Softmax in combination with NLLLoss = CrossEntropy loss .
# check if GPU is available
device = 'cuda' if torch.cuda.is_available() else 'cpu'
embedding_dim=10 # you can change, if you want
model = SkipGram(len(vocab_to_int), embedding_dim).to(device)
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
print_every = 1
steps = 0
epochs = 2
# train for some number of epochs
for e in range(epochs):
# get input and target batches
for inputs, targets in get_batches(train_words, 512):
steps += 1
inputs, targets = torch.LongTensor(inputs), torch.LongTensor(targets)
inputs, targets = inputs.to(device), targets.to(device)
log_ps = model(inputs)
loss = criterion(log_ps, targets)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if steps % print_every == 0:
# getting examples and similarities
valid_examples, valid_similarities = cosine_similarity(model.embed, device=device)
_, closest_idxs = valid_similarities.topk(6) # topk highest similarities
valid_examples, closest_idxs = valid_examples.to('cpu'), closest_idxs.to('cpu')
for ii, valid_idx in enumerate(valid_examples):
closest_words = [int_to_vocab[idx.item()] for idx in closest_idxs[ii]][1:]
print(int_to_vocab[valid_idx.item()] + " | " + ', '.join(closest_words))
print("...")
break
break
print("\nCPU source is used out, die...\n")but | pixels, dracula, buckling, weights, shifting
all | bodhi, catamarans, terrors, illustrators, carousel
an | chemotherapy, occultations, influenced, municipally, chants
years | meditations, gush, inevitability, uncircumcised, intensive
that | lecturer, nicer, kyle, workplace, paragraph
while | randomly, playlist, bennett, raincoat, bitterness
was | northland, multipurpose, discoverer, naboth, porco
between | orchards, pitt, carries, admiration, flexed
smith | overabundance, smell, mcknight, notional, amin
primarily | treated, hijacked, radhakrishnan, gauthier, larry
consists | myself, luang, railtrack, weren, lessen
http | sparta, boineburg, novak, brussel, overruns
question | crushed, junichiro, oversimplification, dheas, handbook
event | overillumination, medica, aldehydes, reconstructing, asterales
channel | fluffy, buff, dynamic, shmuel, promptly
prince | violin, micrometre, arms, mdma, already
...Visualizing the word vectors
Below we'll use T-SNE to visualize how our high-dimensional word vectors cluster together. T-SNE is used to project these vectors into two dimensions while preserving local stucture. Check out this post from Christopher Olah to learn more about T-SNE and other ways to visualize high-dimensional data.
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE# getting embeddings from the embedding layer of our model, by name
embeddings = model.embed.weight.to('cpu').data.numpy()viz_words = 600
tsne = TSNE()
embed_tsne = tsne.fit_transform(embeddings[:viz_words, :])fig, ax = plt.subplots(figsize=(16, 16))
for idx in range(viz_words):
plt.scatter(*embed_tsne[idx, :], color='steelblue')
plt.annotate(int_to_vocab[idx], (embed_tsne[idx, 0], embed_tsne[idx, 1]), alpha=0.7)
utils.py
import re
from collections import Counter
def preprocess(text):
# Replace punctuation with tokens so we can use them in our model
text = text.lower()
text = text.replace('.', ' <PERIOD> ')
text = text.replace(',', ' <COMMA> ')
text = text.replace('"', ' <QUOTATION_MARK> ')
text = text.replace(';', ' <SEMICOLON> ')
text = text.replace('!', ' <EXCLAMATION_MARK> ')
text = text.replace('?', ' <QUESTION_MARK> ')
text = text.replace('(', ' <LEFT_PAREN> ')
text = text.replace(')', ' <RIGHT_PAREN> ')
text = text.replace('--', ' <HYPHENS> ')
text = text.replace('?', ' <QUESTION_MARK> ')
# text = text.replace('\n', ' <NEW_LINE> ')
text = text.replace(':', ' <COLON> ')
words = text.split()
# Remove all words with 5 or fewer occurences
word_counts = Counter(words)
trimmed_words = [word for word in words if word_counts[word] > 5]
return trimmed_words
def create_lookup_tables(words):
"""
Create lookup tables for vocabulary
:param words: Input list of words
:return: Two dictionaries, vocab_to_int, int_to_vocab
"""
word_counts = Counter(words)
# sorting the words from most to least frequent in text occurrence
sorted_vocab = sorted(word_counts, key=word_counts.get, reverse=True)
# create int_to_vocab dictionaries
int_to_vocab = {ii: word for ii, word in enumerate(sorted_vocab)}
vocab_to_int = {word: ii for ii, word in int_to_vocab.items()}
return vocab_to_int, int_to_vocab
二次抽样算丢弃率
Subsampling equation
$$ P(w_i) = 1 - \sqrt{\frac{t}{f(w_i)}} $$
For the following quiz question, consider the following data points:
- We have a text with 1 million words in it
- The word "learn" appears 700 times in this text

计算公式:
Yes! 1-sqrt((110^-4)/(700/(110^6))) = 0.622
为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



