AI For Trading:Backtesting project 8 (120)
Project 8: Backtesting
In this project, you will build a fairly realistic backtester that uses the Barra data. The backtester will perform portfolio optimization that includes transaction costs, and you'll implement it with computational efficiency in mind, to allow for a reasonably fast backtest. You'll also use performance attribution to identify the major drivers of your portfolio's profit-and-loss (PnL). You will have the option to modify and customize the backtest as well.
Instructions
Each problem consists of a function to implement and instructions on how to implement the function. The parts of the function that need to be implemented are marked with a # TODO comment. Your code will be checked for the correct solution when you submit it to Udacity.
Packages
When you implement the functions, you'll only need to you use the packages you've used in the classroom, like Pandas and Numpy. These packages will be imported for you. We recommend you don't add any import statements, otherwise the grader might not be able to run your code.
Install Packages
import sys
!{sys.executable} -m pip install -r requirements.txtRequirement already satisfied: matplotlib==2.1.0 in /opt/conda/lib/python3.6/site-packages (from -r requirements.txt (line 1)) (2.1.0)
Requirement already satisfied: numpy==1.16.1 in /opt/conda/lib/python3.6/site-packages (from -r requirements.txt (line 2)) (1.16.1)
Requirement already satisfied: cycler>=0.10 in /opt/conda/lib/python3.6/site-packages/cycler-0.10.0-py3.6.egg (from matplotlib==2.1.0->-r requirements.txt (line 1)) (0.10.0)
Requirement already satisfied: pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.1 in /opt/conda/lib/python3.6/site-packages (from matplotlib==2.1.0->-r requirements.txt (line 1)) (2.2.0)Load Packages
import scipy
import patsy
import pickle
import numpy as np
import pandas as pd
import scipy.sparse
import matplotlib.pyplot as plt
from statistics import median
from scipy.stats import gaussian_kde
from statsmodels.formula.api import ols
from tqdm import tqdmLoad Data
We’ll be using the Barra dataset to get factors that can be used to predict risk. Loading and parsing the raw Barra data can be a very slow process that can significantly slow down your backtesting. For this reason, it's important to pre-process the data beforehand. For your convenience, the Barra data has already been pre-processed for you and saved into pickle files. You will load the Barra data from these pickle files.
In the code below, we start by loading 2004 factor data from the pandas-frames.2004.pickle file. We also load the 2003 and 2004 covariance data from the covaraince.2003.pickle and covaraince.2004.pickle files. You are encouraged to customize the data range for your backtest. For example, we recommend starting with two or three years of factor data. Remember that the covariance data should include all the years that you choose for the factor data, and also one year earlier. For example, in the code below we are using 2004 factor data, therefore, we must include 2004 in our covariance data, but also the previous year, 2003. If you don't remember why must include this previous year, feel free to review the lessons.
barra_dir = '../../data/project_8_barra/'
data = {}
for year in [2004]:
fil = barra_dir + "pandas-frames." + str(year) + ".pickle"
data.update(pickle.load( open( fil, "rb" ) ))
covariance = {}
for year in [2004]:
fil = barra_dir + "covariance." + str(year) + ".pickle"
covariance.update(pickle.load( open(fil, "rb" ) ))
daily_return = {}
for year in [2004, 2005]:
fil = barra_dir + "price." + str(year) + ".pickle"
daily_return.update(pickle.load( open(fil, "rb" ) ))Shift Daily Returns Data (TODO)
In the cell below, we want to incorporate a realistic time delay that exists in live trading, we’ll use a two day delay for the daily_return data. That means the daily_return should be two days after the data in data and cov_data. Combine daily_return and data together in a dict called frames.
Since reporting of PnL is usually for the date of the returns, make sure to use the two day delay dates (dates that match the daily_return) when building frames. This means calling frames['20040108'] will get you the prices from "20040108" and the data from data at "20040106".
Note: We're not shifting covariance, since we'll use the "DataDate" field in frames to lookup the covariance data. The "DataDate" field contains the date when the data in frames was recorded. For example, frames['20040108'] will give you a value of "20040106" for the field "DataDate".
frames ={}
dlyreturn_n_days_delay = 2
# TODO: Implement
data_date_l = sorted(data.keys())
# print(data_date_1)
return_date_l = sorted(daily_return.keys())
# print(return_date_l)
return_date_l_shifted = return_date_l[dlyreturn_n_days_delay:len(data)+dlyreturn_n_days_delay]
date_l = zip(data_date_l,return_date_l_shifted)
# pirnt(date_1)
for data_date, return_date in date_l:
frames[return_date] = data[data_date].merge(daily_return[return_date],on='Barrid')Add Daily Returns date column (Optional)
Name the column DlyReturnDate.
Hint: create a list containing copies of the date, then create a pandas series.
# Optional
for DlyReturnDate,df in daily_return.items():
n_row = df.shape[0]
df['DlyReturnDate'] = pd.Series([DlyReturnDate]*n_row)Winsorize
As we have done in other projects, we'll want to avoid extremely positive or negative values in our data. Will therefore create a function, wins, that will clip our values to a minimum and maximum range. This process is called Winsorizing. Remember that this helps us handle noise, which may otherwise cause unusually large positions.
def wins(x,a,b):
return np.where(x <= a,a, np.where(x >= b, b, x))Density Plot
Let's check our wins function by taking a look at the distribution of returns for a single day 20040102. We will clip our data from -0.1 to 0.1 and plot it using our density_plot function.
def density_plot(data):
density = gaussian_kde(data)
xs = np.linspace(np.min(data),np.max(data),200)
density.covariance_factor = lambda : .25
density._compute_covariance()
plt.plot(xs,density(xs))
plt.xlabel('Daily Returns')
plt.ylabel('Density')
plt.show()
test = frames['20040108']
test['DlyReturn'] = wins(test['DlyReturn'],-0.1,0.1)
density_plot(test['DlyReturn'])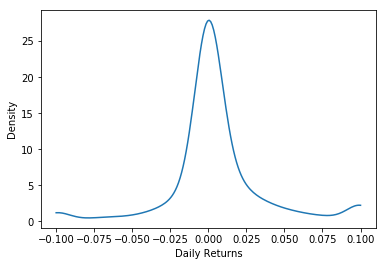
Factor Exposures and Factor Returns
Recall that:
$r{i,t} = \sum{j=1}^{k} (\beta{i,j,t-2} \times f{j,t})$
where $i=1...N$ (N assets),
and $j=1...k$ (k factors).
where $r{i,t}$ is the return, $\beta{i,j,t-2}$ is the factor exposure, and $f{j,t}$ is the factor return. Since we get the factor exposures from the Barra data, and we know the returns, it is possible to estimate the factor returns. In this notebook, we will use the Ordinary Least Squares (OLS) method to estimate the factor exposures, $f{j,t}$, by using $\beta{i,j,t-2}$ as the independent variable, and $r{i,t}$ as the dependent variable.
def get_formula(factors, Y):
L = ["0"]
L.extend(factors)
return Y + " ~ " + " + ".join(L)
def factors_from_names(n):
return list(filter(lambda x: "USFASTD_" in x, n))
def estimate_factor_returns(df):
## build universe based on filters
estu = df.loc[df.IssuerMarketCap > 1e9].copy(deep=True)
## winsorize returns for fitting
estu['DlyReturn'] = wins(estu['DlyReturn'], -0.25, 0.25)
all_factors = factors_from_names(list(df))
form = get_formula(all_factors, "DlyReturn")
model = ols(form, data=estu)
results = model.fit()
return resultsfacret = {}
for date in frames:
facret[date] = estimate_factor_returns(frames[date]).paramsmy_dates = sorted(list(map(lambda date: pd.to_datetime(date, format='%Y%m%d'), frames.keys())))Choose Alpha Factors
We will now choose our alpha factors. Barra's factors include some alpha factors that we have seen before, such as:
-
USFASTD_1DREVRSL : Reversal
-
USFASTD_EARNYILD : Earnings Yield
-
USFASTD_VALUE : Value
-
USFASTD_SENTMT : Sentiment
We will choose these alpha factors for now, but you are encouraged to come back to this later and try other factors as well.
alpha_factors = ["USFASTD_1DREVRSL", "USFASTD_EARNYILD", "USFASTD_VALUE", "USFASTD_SENTMT"]
facret_df = pd.DataFrame(index = my_dates)
for dt in my_dates:
for alp in alpha_factors:
facret_df.at[dt, alp] = facret[dt.strftime('%Y%m%d')][alp]
for column in facret_df.columns:
plt.plot(facret_df[column].cumsum(), label=column)
plt.legend(loc='upper left')
plt.xlabel('Date')
plt.ylabel('Cumulative Factor Returns')
plt.show()/opt/conda/lib/python3.6/site-packages/pandas/plotting/_converter.py:129: FutureWarning: Using an implicitly registered datetime converter for a matplotlib plotting method. The converter was registered by pandas on import. Future versions of pandas will require you to explicitly register matplotlib converters.
To register the converters:
>>> from pandas.plotting import register_matplotlib_converters
>>> register_matplotlib_converters()
warnings.warn(msg, FutureWarning)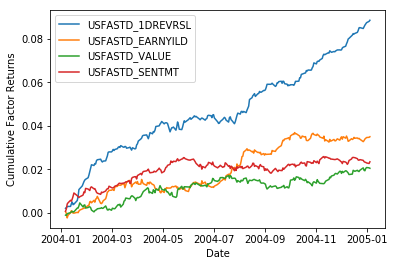
Merge Previous Portfolio Holdings
In order to optimize our portfolio we will use the previous day's holdings to estimate the trade size and transaction costs. In order to keep track of the holdings from the previous day we will include a column to hold the portfolio holdings of the previous day. These holdings of all our assets will be initialized to zero when the backtest first starts.
def clean_nas(df):
numeric_columns = df.select_dtypes(include=[np.number]).columns.tolist()
for numeric_column in numeric_columns:
df[numeric_column] = np.nan_to_num(df[numeric_column])
return dfprevious_holdings = pd.DataFrame(data = {"Barrid" : ["USA02P1"], "h.opt.previous" : np.array(0)})
df = frames[my_dates[0].strftime('%Y%m%d')]
df = df.merge(previous_holdings, how = 'left', on = 'Barrid')
df = clean_nas(df)
df.loc[df['SpecRisk'] == 0]['SpecRisk'] = median(df['SpecRisk'])Build Universe Based on Filters (TODO)
In the cell below, implement the function get_universe that creates a stock universe by selecting only those companies that have a market capitalization of at least 1 billion dollars OR that are in the previous day's holdings, even if on the current day, the company no longer meets the 1 billion dollar criteria.
When creating the universe, make sure you use the .copy() attribute to create a copy of the data. Also, it is very important to make sure that we are not looking at returns when forming the portfolio! to make this impossible, make sure to drop the column containing the daily return.
def get_universe(df):
"""
Create a stock universe based on filters
Parameters
----------
df : DataFrame
All stocks
Returns
-------
universe : DataFrame
Selected stocks based on filters
"""
# TODO: Implement
universe = df.loc[(df['IssuerMarketCap'] >= 1e9) | (abs(df['h.opt.previous']) > 0)].copy()
universe = universe.drop(columns = 'DlyReturn')
return universe
universe = get_universe(df)date = str(int(universe['DataDate'][1])) Factors
We will now extract both the risk factors and alpha factors. We begin by first getting all the factors using the factors_from_names function defined previously.
all_factors = factors_from_names(list(universe))We will now create the function setdiff to just select the factors that we have not defined as alpha factors
def setdiff(temp1, temp2):
s = set(temp2)
temp3 = [x for x in temp1 if x not in s]
return temp3risk_factors = setdiff(all_factors, alpha_factors)We will also save the column that contains the previous holdings in a separate variable because we are going to use it later when we perform our portfolio optimization.
h0 = universe['h.opt.previous']Matrix of Risk Factor Exposures
Our dataframe contains several columns that we'll use as risk factors exposures. Extract these and put them into a matrix.
The data, such as industry category, are already one-hot encoded, but if this were not the case, then using patsy.dmatrices would help, as this function extracts categories and performs the one-hot encoding. We'll practice using this package, as you may find it useful with future data sets. You could also store the factors in a dataframe if you prefer.
How to use patsy.dmatrices
patsy.dmatrices takes in a formula and the dataframe. The formula tells the function which columns to take. The formula will look something like this:SpecRisk ~ 0 + USFASTD_AERODEF + USFASTD_AIRLINES + ...
where the variable to the left of the ~ is the "dependent variable" and the others to the right are the independent variables (as if we were preparing data to be fit to a model).
This just means that the pasty.dmatrices function will return two matrix variables, one that contains the single column for the dependent variable outcome, and the independent variable columns are stored in a matrix predictors.
The predictors matrix will contain the matrix of risk factors, which is what we want. We don't actually need the outcome matrix; it's just created because that's the way patsy.dmatrices works.
formula = get_formula(risk_factors, "SpecRisk")def model_matrix(formula, data):
outcome, predictors = patsy.dmatrices(formula, data)
return predictorsB = model_matrix(formula, universe)
BT = B.transpose()Calculate Specific Variance
Notice that the specific risk data is in percent:
universe['SpecRisk'][0:2]0 9.014505
1 11.726327
Name: SpecRisk, dtype: float64Therefore, in order to get the specific variance for each stock in the universe we first need to multiply these values by 0.01 and then square them:
specVar = (0.01 * universe['SpecRisk']) ** 2Factor covariance matrix (TODO)
Note that we already have factor covariances from Barra data, which is stored in the variable covariance. covariance is a dictionary, where the key is each day's date, and the value is a dataframe containing the factor covariances.
covariance['20040102'].head()| Factor1 | Factor2 | VarCovar | DataDate | |
|---|---|---|---|---|
| 0 | USFASTD_1DREVRSL | USFASTD_1DREVRSL | 1.958869 | 20040102 |
| 1 | USFASTD_1DREVRSL | USFASTD_BETA | 1.602458 | 20040102 |
| 2 | USFASTD_1DREVRSL | USFASTD_DIVYILD | -0.012642 | 20040102 |
| 3 | USFASTD_1DREVRSL | USFASTD_DWNRISK | -0.064387 | 20040102 |
| 4 | USFASTD_1DREVRSL | USFASTD_EARNQLTY | 0.046573 | 20040102 |
In the code below, implement the function diagonal_factor_cov to create the factor covariance matrix. Note that the covariances are given in percentage units squared. Therefore you must re-scale them appropriately so that they're in decimals squared. Use the given colnames function to get the column names from B.
When creating factor covariance matrix, you can store the factor variances and covariances, or just store the factor variances. Try both, and see if you notice any differences.
def colnames(B):
if type(B) == patsy.design_info.DesignMatrix:
return B.design_info.column_names
if type(B) == pandas.core.frame.DataFrame:
return B.columns.tolist()
return Nonedef diagonal_factor_cov(date, B):
"""
Create the factor covariance matrix
Parameters
----------
date : string
date. For example 20040102
B : patsy.design_info.DesignMatrix OR pandas.core.frame.DataFrame
Matrix of Risk Factors
Returns
-------
Fm : Numpy ndarray
factor covariance matrix
"""
# TODO: Implement
cv = covariance[date]
k = np.shape(B)[1]
Fm = np.zeros([k,k])
for j in range(0,k):
fac = colnames(B)[j]
Fm[j,j] = (0.01**2) * cv.loc[(cv.Factor1==fac) & (cv.Factor2==fac),"VarCovar"].iloc[0]
return Fm
Fvar = diagonal_factor_cov(date, B)Transaction Costs
To get the transaction cost, or slippage, we have to multiply the price change due to market impact by the amount of dollars traded:
$$
\mbox{tcost{i,t}} = \% \Delta \mbox{price}{i,t} \times \mbox{trade}_{i,t}
$$
In summation notation it looks like this:
$$
\mbox{tcost}_{i,t} = \sumi^{N} \lambda{i,t} (h{i,t} - h{i,t-1})^2
$$
where
$$
\lambda{i,t} = \frac{1}{10\times \mbox{ADV}{i,t}}
$$
Note that since we're dividing by ADV, we'll want to handle cases when ADV is missing or zero. In those instances, we can set ADV to a small positive number, such as 10,000, which, in practice assumes that the stock is illiquid. In the code below if there is no volume information we assume the asset is illiquid.
def get_lambda(universe, composite_volume_column = 'ADTCA_30'):
universe.loc[np.isnan(universe[composite_volume_column]), composite_volume_column] = 1.0e4
universe.loc[universe[composite_volume_column] == 0, composite_volume_column] = 1.0e4
adv = universe[composite_volume_column]
return 0.1 / adv
Lambda = get_lambda(universe)Alpha Combination (TODO)
In the code below create a matrix of alpha factors and return it from the function get_B_alpha. Create this matrix in the same way you created the matrix of risk factors, i.e. using the get_formula and model_matrix functions we have defined above. Feel free to go back and look at the previous code.
def get_B_alpha(alpha_factors, universe):
# TODO: Implement
res = model_matrix(get_formula(alpha_factors, "SpecRisk"), data = universe)
return res
B_alpha = get_B_alpha(alpha_factors, universe)Now that you have the matrix containing the alpha factors we will combine them by adding its rows. By doing this we will collapse the B_alpha matrix into a single alpha vector. We'll multiply by 1e-4 so that the expression of expected portfolio return, $\alpha^T \mathbf{h}$, is in dollar units.
def get_alpha_vec(B_alpha):
"""
Create an alpha vecrtor
Parameters
----------
B_alpha : patsy.design_info.DesignMatrix
Matrix of Alpha Factors
Returns
-------
alpha_vec : patsy.design_info.DesignMatrix
alpha vecrtor
"""
# TODO: Implement
scale = 1e-4
alpha_vec = scale * np.sum(B_alpha, axis=1)
# test
print(alpha_vec);
return alpha_vec
alpha_vec = get_alpha_vec(B_alpha)[-6.080e-05 -2.768e-04 -3.630e-05 ... 1.900e-06 1.679e-04 3.930e-05]Optional Challenge
You can also try to a more sophisticated method of alpha combination, by choosing the holding for each alpha based on the same metric of its performance, such as the factor returns, or sharpe ratio. To make this more realistic, you can calculate a rolling average of the sharpe ratio, which is updated for each day. Remember to only use data that occurs prior to the date of each optimization, and not data that occurs in the future. Also, since factor returns and sharpe ratios may be negative, consider using a max function to give the holdings a lower bound of zero.
Objective function (TODO)
The objective function is given by:
$$
f(\mathbf{h}) = \frac{1}{2}\kappa \mathbf{h}_t^T\mathbf{Q}^T\mathbf{Q}\mathbf{h}_t + \frac{1}{2} \kappa \mathbf{h}_t^T \mathbf{S} \mathbf{h}_t - \mathbf{\alpha}^T \mathbf{h}t + (\mathbf{h}{t} - \mathbf{h}{t-1})^T \mathbf{\Lambda} (\mathbf{h}{t} - \mathbf{h}_{t-1})
$$
Where the terms correspond to: factor risk + idiosyncratic risk - expected portfolio return + transaction costs, respectively. We should also note that $\textbf{Q}^T\textbf{Q}$ is defined to be the same as $\textbf{BFB}^T$. Review the lessons if you need a refresher of how we get $\textbf{Q}$.
Our objective is to minimize this objective function. To do this, we will use Scipy's optimization function:
scipy.optimize.fmin_l_bfgs_b(func, initial_guess, func_gradient)
where:
-
func : is the function we want to minimize
-
initial_guess : is out initial guess
-
func_gradient : is the gradient of the function we want to minimize
So, in order to use the scipy.optimize.fmin_l_bfgs_b function we first need to define its parameters.
In the code below implement the function obj_func(h) that corresponds to the objective function above that we want to minimize. We will set the risk aversion to be 1.0e-6.
risk_aversion = 1.0e-6
def get_obj_func(h0, risk_aversion, Q, specVar, alpha_vec, Lambda):
def obj_func(h):
# TODO: Implement
f = 0.0
f += 0.5 * risk_aversion * np.sum( np.matmul(Q, h) ** 2 )
f += 0.5 * risk_aversion * np.dot(h ** 2, specVar) #since Specific Variance is diagonal, don't have to do matmul
f -= np.dot(h, alpha_vec)
# print(f)
f += np.dot( (h - h0) ** 2, Lambda)
# print(f)
return f
return obj_funcGradient (TODO)
Now that we can generate the objective function using get_obj_func, we can now create a similar function with its gradient. The reason we're interested in calculating the gradient is so that we can tell the optimizer in which direction, and how much, it should shift the portfolio holdings in order to improve the objective function (minimize variance, minimize transaction cost, and maximize expected portfolio return).
Before we implement the function we first need to know what the gradient looks like. The gradient, or derivative of the objective function, with respect to the portfolio holdings h, is given by:
$$
f'(\mathbf{h}) = \frac{1}{2}\kappa (2\mathbf{Q}^T\mathbf{Qh}) + \frac{1}{2}\kappa (2\mathbf{Sh}) - \mathbf{\alpha} + 2(\mathbf{h}{t} - \mathbf{h}{t-1}) \mathbf{\Lambda}
$$
In the code below, implement the function grad(h) that corresponds to the function of the gradient given above.
def get_grad_func(h0, risk_aversion, Q, QT, specVar, alpha_vec, Lambda):
def grad_func(h):
# TODO: Implement
g = risk_aversion * (np.matmul(QT, np.matmul(Q,h)) + (specVar * h) ) - alpha_vec + 2 * (h-h0) * Lambda
return np.asarray(g)
return grad_funcOptimize (TODO)
Now that we can generate the objective function using get_obj_func, and its corresponding gradient using get_grad_func we are ready to minimize the objective function using Scipy's optimization function. For this, we will use out initial holdings as our initial_guess parameter.
In the cell below, implement the function get_h_star that optimizes the objective function. Use the objective function (obj_func) and gradient function (grad_func) provided within get_h_star to optimize the objective function using the scipy.optimize.fmin_l_bfgs_b function.
risk_aversion = 1.0e-6
Q = np.matmul(scipy.linalg.sqrtm(Fvar), BT)
QT = Q.transpose()
def get_h_star(risk_aversion, Q, QT, specVar, alpha_vec, h0, Lambda):
"""
Optimize the objective function
Parameters
----------
risk_aversion : int or float
Trader's risk aversion
Q : patsy.design_info.DesignMatrix
Q Matrix
QT : patsy.design_info.DesignMatrix
Transpose of the Q Matrix
specVar: Pandas Series
Specific Variance
alpha_vec: patsy.design_info.DesignMatrix
alpha vector
h0 : Pandas Series
initial holdings
Lambda : Pandas Series
Lambda
Returns
-------
optimizer_result[0]: Numpy ndarray
optimized holdings
"""
obj_func = get_obj_func(h0, risk_aversion, Q, specVar, alpha_vec, Lambda)
grad_func = get_grad_func(h0, risk_aversion, Q, QT, specVar, alpha_vec, Lambda)
# TODO: Implement
optimizer_result = scipy.optimize.fmin_l_bfgs_b(obj_func, h0, fprime=grad_func)
# print(optimizer_result)
return optimizer_result[0]
h_star = get_h_star(risk_aversion, Q, QT, specVar, alpha_vec, h0, Lambda)After we have optimized our objective function we can now use, h_star to create our optimal portfolio:
opt_portfolio = pd.DataFrame(data = {"Barrid" : universe['Barrid'], "h.opt" : h_star})Risk Exposures (TODO)
We can also use h_star to calculate our portfolio's risk and alpha exposures.
In the cells below implement the functions get_risk_exposures and get_portfolio_alpha_exposure that calculate the portfolio's risk and alpha exposures, respectively.
def get_risk_exposures(B, BT, h_star):
"""
Calculate portfolio's Risk Exposure
Parameters
----------
B : patsy.design_info.DesignMatrix
Matrix of Risk Factors
BT : patsy.design_info.DesignMatrix
Transpose of Matrix of Risk Factors
h_star: Numpy ndarray
optimized holdings
Returns
-------
risk_exposures : Pandas Series
Risk Exposures
"""
# TODO: Implement
risk_exposures = np.matmul(BT, h_star)
return pd.Series(risk_exposures, index = colnames(B))
risk_exposures = get_risk_exposures(B, BT, h_star)def get_portfolio_alpha_exposure(B_alpha, h_star):
"""
Calculate portfolio's Alpha Exposure
Parameters
----------
B_alpha : patsy.design_info.DesignMatrix
Matrix of Alpha Factors
h_star: Numpy ndarray
optimized holdings
Returns
-------
alpha_exposures : Pandas Series
Alpha Exposures
"""
# TODO: Implement
alpha_exposures = np.matmul(B_alpha.transpose(), h_star)
return pd.Series(np.matmul(B_alpha.transpose(), h_star), index = colnames(B_alpha))
portfolio_alpha_exposure = get_portfolio_alpha_exposure(B_alpha, h_star)Transaction Costs (TODO)
We can also use h_star to calculate our total transaction costs:
$$
\mbox{tcost} = \sumi^{N} \lambda{i} (h{i,t} - h{i,t-1})^2
$$
In the cell below, implement the function get_total_transaction_costs that calculates the total transaction costs according to the equation above:
def get_total_transaction_costs(h0, h_star, Lambda):
"""
Calculate Total Transaction Costs
Parameters
----------
h0 : Pandas Series
initial holdings (before optimization)
h_star: Numpy ndarray
optimized holdings
Lambda : Pandas Series
Lambda
Returns
-------
total_transaction_costs : float
Total Transaction Costs
"""
total_transaction_costs = np.dot( (h_star - h0) ** 2, Lambda)
# print(Lambda)
# print(total_transaction_costs)
return total_transaction_costs
total_transaction_costs = get_total_transaction_costs(h0, h_star, Lambda)
print(total_transaction_costs)104.87520269773562Putting It All Together
We can now take all the above functions we created above and use them to create a single function, form_optimal_portfolio that returns the optimal portfolio, the risk and alpha exposures, and the total transactions costs.
def form_optimal_portfolio(df, previous, risk_aversion):
df = df.merge(previous, how = 'left', on = 'Barrid')
df = clean_nas(df)
df.loc[df['SpecRisk'] == 0]['SpecRisk'] = median(df['SpecRisk'])
universe = get_universe(df)
date = str(int(universe['DataDate'][1]))
all_factors = factors_from_names(list(universe))
risk_factors = setdiff(all_factors, alpha_factors)
h0 = universe['h.opt.previous']
B = model_matrix(get_formula(risk_factors, "SpecRisk"), universe)
BT = B.transpose()
specVar = (0.01 * universe['SpecRisk']) ** 2
Fvar = diagonal_factor_cov(date, B)
Lambda = get_lambda(universe)
B_alpha = get_B_alpha(alpha_factors, universe)
alpha_vec = get_alpha_vec(B_alpha)
Q = np.matmul(scipy.linalg.sqrtm(Fvar), BT)
QT = Q.transpose()
h_star = get_h_star(risk_aversion, Q, QT, specVar, alpha_vec, h0, Lambda)
opt_portfolio = pd.DataFrame(data = {"Barrid" : universe['Barrid'], "h.opt" : h_star})
risk_exposures = get_risk_exposures(B, BT, h_star)
portfolio_alpha_exposure = get_portfolio_alpha_exposure(B_alpha, h_star)
total_transaction_costs = get_total_transaction_costs(h0, h_star, Lambda)
return {
"opt.portfolio" : opt_portfolio,
"risk.exposures" : risk_exposures,
"alpha.exposures" : portfolio_alpha_exposure,
"total.cost" : total_transaction_costs}Build tradelist
The trade list is the most recent optimal asset holdings minus the previous day's optimal holdings.
def build_tradelist(prev_holdings, opt_result):
tmp = prev_holdings.merge(opt_result['opt.portfolio'], how='outer', on = 'Barrid')
tmp['h.opt.previous'] = np.nan_to_num(tmp['h.opt.previous'])
tmp['h.opt'] = np.nan_to_num(tmp['h.opt'])
return tmpSave optimal holdings as previous optimal holdings.
As we walk through each day, we'll re-use the column for previous holdings by storing the "current" optimal holdings as the "previous" optimal holdings.
def convert_to_previous(result):
prev = result['opt.portfolio']
prev = prev.rename(index=str, columns={"h.opt": "h.opt.previous"}, copy=True, inplace=False)
return prevRun the backtest
Walk through each day, calculating the optimal portfolio holdings and trade list. This may take some time, but should finish sooner if you've chosen all the optimizations you learned in the lessons.
trades = {}
port = {}
for dt in tqdm(my_dates, desc='Optimizing Portfolio', unit='day'):
date = dt.strftime('%Y%m%d')
result = form_optimal_portfolio(frames[date], previous_holdings, risk_aversion)
trades[date] = build_tradelist(previous_holdings, result)
port[date] = result
previous_holdings = convert_to_previous(result)Optimizing Portfolio: 0%| | 0/252 [00:00<?, ?day/s]
[-6.080e-05 -2.768e-04 -3.630e-05 ... 1.900e-06 1.679e-04 3.930e-05]
Optimizing Portfolio: 0%| | 1/252 [00:06<28:48, 6.89s/day]
[-3.240e-05 -3.286e-04 -1.297e-04 ... 1.381e-04 -3.500e-05 5.640e-05]
Optimizing Portfolio: 1%| | 2/252 [00:13<29:05, 6.98s/day]
[-1.150e-04 -3.690e-04 -9.100e-05 ... 3.990e-05 1.379e-04 5.360e-05]
Optimizing Portfolio: 100%|██████████| 252/252 [26:40<00:00, 6.35s/day]Profit-and-Loss (PnL) attribution (TODO)
Profit and Loss is the aggregate realized daily returns of the assets, weighted by the optimal portfolio holdings chosen, and summed up to get the portfolio's profit and loss.
The PnL attributed to the alpha factors equals the factor returns times factor exposures for the alpha factors.
$$
\mbox{PnL}{alpha}= f \times b{alpha}
$$
Similarly, the PnL attributed to the risk factors equals the factor returns times factor exposures of the risk factors.
$$
\mbox{PnL}{risk} = f \times b{risk}
$$
In the code below, in the function build_pnl_attribution calculate the PnL attributed to the alpha factors, the PnL attributed to the risk factors, and attribution to cost.
## assumes v, w are pandas Series
def partial_dot_product(v, w):
common = v.index.intersection(w.index)
return np.sum(v[common] * w[common])
def build_pnl_attribution():
df = pd.DataFrame(index = my_dates)
for dt in my_dates:
date = dt.strftime('%Y%m%d')
p = port[date]
fr = facret[date]
mf = p['opt.portfolio'].merge(frames[date], how = 'left', on = "Barrid")
mf['DlyReturn'] = wins(mf['DlyReturn'], -0.5, 0.5)
df.at[dt,"daily.pnl"] = np.sum(mf['h.opt'] * mf['DlyReturn'])
# TODO: Implement
df.at[dt,"attribution.alpha.pnl"] = partial_dot_product(fr, p['alpha.exposures'])
df.at[dt,"attribution.risk.pnl"] = partial_dot_product(fr, p['risk.exposures'])
df.at[dt,"attribution.cost"] = p['total.cost']
return dfattr = build_pnl_attribution()
for column in attr.columns:
plt.plot(attr[column].cumsum(), label=column)
plt.legend(loc='upper left')
plt.xlabel('Date')
plt.ylabel('PnL Attribution')
plt.show()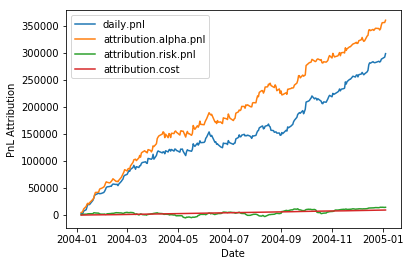
Build portfolio characteristics (TODO)
Calculate the sum of long positions, short positions, net positions, gross market value, and amount of dollars traded.
In the code below, in the function build_portfolio_characteristics calculate the sum of long positions, short positions, net positions, gross market value, and amount of dollars traded.
def build_portfolio_characteristics():
df = pd.DataFrame(index = my_dates)
for dt in my_dates:
date = dt.strftime('%Y%m%d')
p = port[date]
tradelist = trades[date]
h = p['opt.portfolio']['h.opt']
# TODO: Implement
df.at[dt,"long"] = np.sum(h[h>0])
df.at[dt,"short"] = np.sum(h[h<0])
df.at[dt,"net"] = np.sum(h)
df.at[dt,"gmv"] = np.sum(np.abs(h))
df.at[dt,"traded"] = np.sum(np.abs(tradelist['h.opt']-tradelist['h.opt.previous']))
return dfpchar = build_portfolio_characteristics()
for column in pchar.columns:
plt.plot(pchar[column], label=column)
plt.legend(loc='upper left')
plt.xlabel('Date')
plt.ylabel('Portfolio')
plt.show()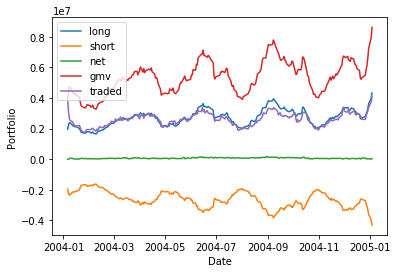
Optional
Choose additional metrics to evaluate your portfolio.
为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



