AI 量化交易:成对交易 (一)
一个基础的算法:成对交易
Timeseries-时间序列
定义:按照时间发生先后顺序排列的数据点序列
作用:可作为离散时间数据进行处理,通常时间间隔为一恒定值(如 1秒,5分钟,1个小时,7天等)
应用领域:应用于绝大多数涉及到时间数据测量的应用科学与工程学。
Stationary-平稳过程
在数学中又称严格平稳(或强平稳),是一种特殊的随机过程。任取一段时间或空间的联合机率分布,与这段期间或空间任意平移后的新期间或空间的联合几率分布相等。这样参数的期望和方差不随时间或位置变化。

Correlation-相关
定义:
- 概率论和统计学->显示两个随机变量之间线性关系的强度和方向
- 统计学->用来衡量两个变量相对于其相互独立的距离->有许多根据数据特点而定义的用来衡量数据相关的系数
相关系数的计算过程:
- 将每个变量都转化为标准单位,乘积的平均数即为相关系数
- 两个变量的关系可以直观地用散点图表示,当期紧密地群聚于一条直线的周围时,变量间存在强相关。

Cointegration-协整
指多个I(1) 的时间序列通过线性组合,可以形成一个I(0)的时间序列。
举例:
- X1, X2, X3 是三个I(1) 序列,以及
2*X1 + X2 + 0 * X3 = 2X1 + X2是 I(0). - 可以看出,X1、X2、X3 是协整关系
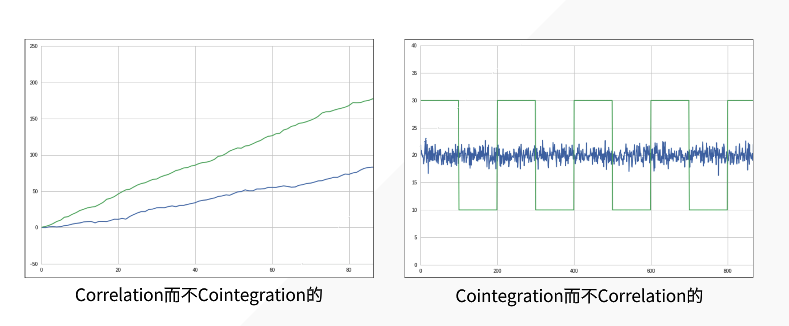
相关和协整的区别

Moving Averages
一套标准来衡量整个历史-这不是一个好策略。
如果市场/社会产生了变化,X和Y组成的这个spread的基准线可能会产生变化。
如果根据过去三年算出了一个基准线,那么,很有可能并不能很完美的表达此刻的世界。所以,Moving Averages只关注一个不断滚动的窗口。每次都计算这个窗口内的基准线(平均值)。
Out of Sample测试
我们虽然很严谨的选取某一段时间内 cointegrate的两个股票 X 和 Y,但是今天的 cointegration,明天还能算数么?
我们要时刻做好测试,保证历史数据对于未来也依旧有参考作用。
这就是我 out of sample 测试,当数据超出我们的样本集时,我们再做一次 cointegration 测试,当 p value 大于阀值得时候,就要及时停止/调整策略。
相关文章:
【机器学习】Moving Averages 滑动平均的原理和直观感知
为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



