协整套利的实现
本文为转载,原文地址 协整套利的实现。
Pairs Trading,即配对交易策略。其基本原理就是找出两只走势相关的股票。这两只股票的价格差距从长期来看在一个固定的水平内波动,如果价差暂时性的超过或低于这个水平,就买多价格偏低的股票,卖空价格偏高的股票。等到价差恢复正常水平时,进行平仓操作,赚取这一过程中价差变化所产生的利润。为了实现协整套利,首先要针对不同的股票时间序列进行协整分析,找到价格走势高度相关的股票对。
协整关系检验函数 coint
在 Python 的 Statsmodels 包中,有直接用于协整关系检验的函数 coint,该函数包含于 statsmodels.tsa.stattools中。
import numpy as np
import pandas as pd
import statsmodels.api as sm
import seaborn as sns首先,我们构造一个读取股票价格,判断协整关系的函数。该函数返回的两个值分别为协整性检验的 p 值矩阵以及所有传入的参数中协整性较强的股票对。我们不需要在意 p 值具体是什么,可以这么理解它: p 值越低,协整关系就越强;p 值低于 0.05 时,协整关系便非常强。
def find_cointegrated_pairs(dataframe):
# 得到DataFrame长度
n = dataframe.shape[1]
# 初始化p值矩阵
pvalue_matrix = np.ones((n, n))
# 抽取列的名称
keys = dataframe.keys()
# 初始化强协整组
pairs = []
# 对于每一个i
for i in range(n):
# 对于大于i的j
for j in range(i+1, n):
# 获取相应的两只股票的价格Series
stock1 = dataframe[keys[i]]
stock2 = dataframe[keys[j]]
# 分析它们的协整关系
result = sm.tsa.stattools.coint(stock1, stock2)
# 取出并记录p值
pvalue = result[1]
pvalue_matrix[i, j] = pvalue
# 如果p值小于0.05
if pvalue < 0.05:
# 记录股票对和相应的p值
pairs.append((keys[i], keys[j], pvalue))
# 返回结果
return pvalue_matrix, pairs然后我们设置要协整分析的股票范围和分析的起止时间范围,我们可以选择画出协整检验热度图,这里画的是1-pvalues,颜色越红表示对应的股票对协整关系越稳定。
instruments =D.instruments()[0:20]
# 确定起始时间
start_date = '2015-01-01'
# 确定结束时间
end_date = '2017-02-18'
# 获取股票总市值数据,返回DataFrame数据格式
prices_temp = D.history_data(instruments,start_date,end_date,
fields=['close'] )
prices_df=pd.pivot_table(prices_temp, values='close', index=['date'], columns=['instrument'])
pvalues, pairs = find_cointegrated_pairs(prices_df)
#画协整检验热度图,输出pvalue < 0.05的股票对
#sns.heatmap(1-pvalues, xticklabels=instruments, yticklabels=instruments, cmap='RdYlGn_r', mask = (pvalues == 1))
#print(pairs)我们对pvalue排序,较小的pvalue表示对应的股票对的协整关系越稳定。
df = pd.DataFrame(pairs, index=range(0,len(pairs)), columns=list(['Name1','Name2','pvalue']))
#pvalue越小表示相关性越大,按pvalue升序排名就是获取相关性从大到小的股票对
df.sort_values(by='pvalue')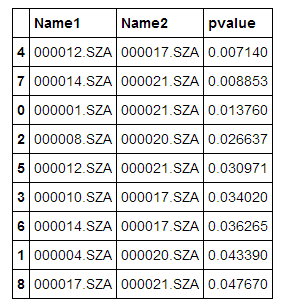
我们选择协整关系最强的一组股票对,绘制走势图并进行最小二乘回归,获取回归系数。
x = prices_df["000012.SZA"]
y = prices_df["000017.SZA"]
plt=x.plot();
plt.plot(y);
X = sm.add_constant(x)
result = (sm.OLS(y,X)).fit()
print(result.summary())
plt.legend(["000012.SZA", "000017.SZA"],loc='best')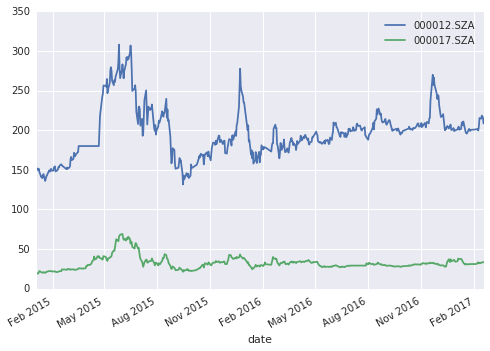
根据获得的回归系数,构造回归方程 y=const+coefx 也就得到y-coefx这个价差平稳序列,画出这个平稳序列可以看出,虽然价差上下波动,但都会回归中间的均值。
接着我们构造z-score函数,计算时间序列偏离了其均值多少倍的标准差
def zscore(series):
return (series - series.mean()) / np.std(series)计算价差的zscore函数序列并绘图
XZ=zscore(0.2048*x-y)
plt=XZ.plot()
plt.axhline(1.0, color="red", linestyle="--")
plt.axhline(-1.0, color="green", linestyle="--")
plt.legend(["z-score", "mean", "+1", "-1"])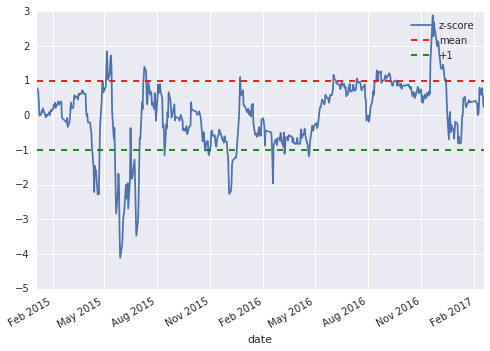
可以看出此序列基本在-1到1之间波动,当两这个序列的 z-score序列 突破 1 或者 −1 时,说明两支股票的价差脱离了统计概念中的合理区间,如果它们的协整关系能够保持,那么它们的价差应该收敛。
结合上图,当 z-score 突破上方红线时,说明y-coefx高估,推测此差值应在未来降低到合理的波动区间,因此可以卖空1份的y标的,买入coef份的x标的,等待y-coefx回归到0附近时平仓获利;反之,当 z-score 突破下方绿线时,说明y-coefx低估,推测此差值应在未来上升加到合理的波动区间,因此可以买入1份的y标的,卖空coef份的x标的,等待y-coefx回归到0附近时平仓获利。
为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



