最小二乘法学习
最小二乘法(又称最小平方法 Ordinary Least Squares)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
变量之间存在着相关关系,比如,人的身高和体重之间存在着关系,一般来说,人高一些,体重要重一些,身高和体重之间存在的是不确定性的相关关系。回归分析是研究相关关系的一种数学工具,它能帮助我们从一个变量的取值区估计另一个变量的取值。
OLS(最小二乘法)主要用于线性回归的参数估计,它的思路很简单,就是求一些使得实际值和模型估值之差的平方和达到最小的值,将其作为参数估计值。就是说,通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法可用于曲线拟合,其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
一,OLS回归
OLS( Ordinary Least Squares) 法通过一系列的预测变量来预测响应变量(也可以说是在预测变量上回归响应变量)。线性回归是指对参数β为线性的一种回归(即参数只以一次方的形式出现)模型:
Yt=α+βxt+μt (t=1……n)表示观测数Yt 被称作因变量
xt 被称作自变量
α、β 为需要最小二乘法去确定的参数,或称回归系数
μt 为随机误差项
OLS线性回归的基本原则:最优拟合曲线应该使各点到直线的距离的平方和(即残差平方和,简称RSS)最小:
OLS线性回归的目标是通过减少响应变量的真实值与预测值的差值来获得模型参数(截距项和斜率),就是使RSS最小。
为了能够恰当地解释OLS模型的系数,数据必须满足以下统计假设:
正态性:对于固定的自变量值,因变量值成正太分布
独立性:个体之间相互独立
线性相关:因变量和自变量之间为线性相关
同方差性:因变量的方差不随自变量的水平不同而变化,即因变量的方差是不变的
二、statsmodels介绍
statsmodels(http://www.statsmodels.org)是一个Python库,用于拟合多种统计模型,执行统计测试以及数据探索和可视化。statsmodels包含更多的“经典”频率学派统计方法,而贝叶斯方法和机器学习模型可在其他库中找到。
包含在statsmodels中的一些模型:
- 线性模型,广义线性模型和鲁棒线性模型
- 线性混合效应模型
- 方差分析(ANOVA)方法
- 时间序列过程和状态空间模型
- 广义的矩量法
在接下来的几页中,我们将在statsmodels中使用一些基本工具,并探讨如何使用带有Patsy公式和pandas DataFrame对象的建模接口。
1、评估线性模型
统计模型中有几种线性回归模型,从较基本的(例如,普通最小二乘)到更复杂的(例如,迭代重新加权的最小二乘)。
1.statsmodels中的线性模型有两个不同的主要接口:基于数组的和基于公式的。这些接口通过这些API模块导入来访问(见图1)
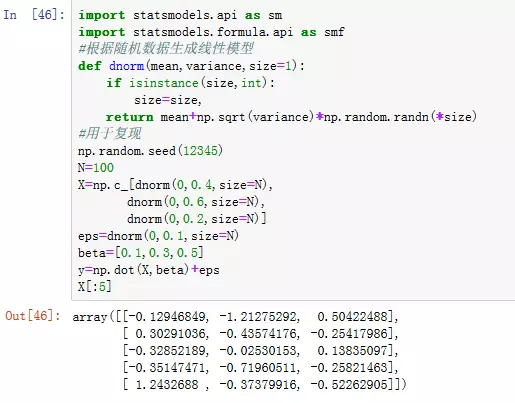
图1:随机数据生成线性模型
注:已知参数beta的“真实”模型。在这种情况下,dnorm是用于生成具有特定均值和方差的正态分布数据的辅助函数。
numpy.dot(a,b,out=None)
Dot product of two arrays. Specifically2.线性模型通常与我们在Patsy中看到的截距项相匹配。sm.add_constant函数可以将截距列添加到现有矩阵。(见图2)
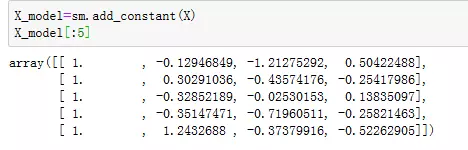
图2:sm.add_constant函数
3.模型的fit方法返回一个回归结果对象,该对象包含了估计的模型参数和其他的诊断(见图3)
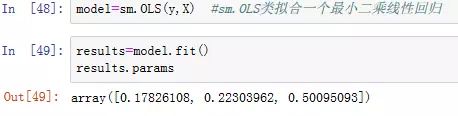
图3:fit方法
4.在results上调用summary方法可以打印出一个模型的诊断细节(见图4)
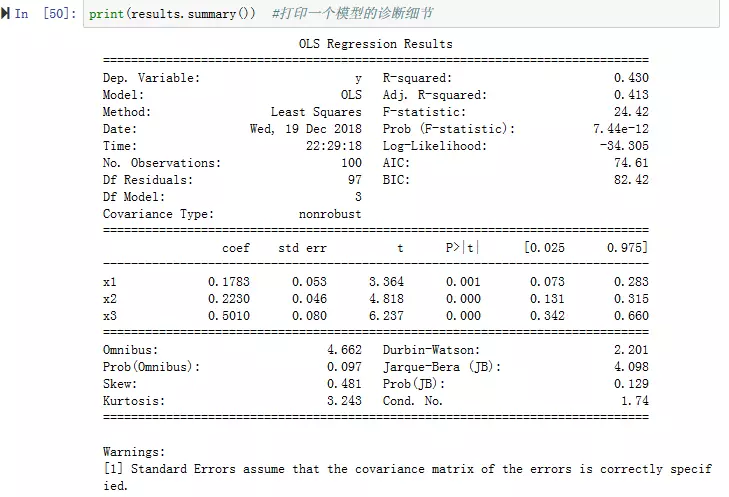
图4:summary方法
5.此处的参数名称已被赋予通用名称x1、x2等。假设所有模型参数都在DataFrame中,使用statsmodels公式API和Patsy公式字符串(见图5)
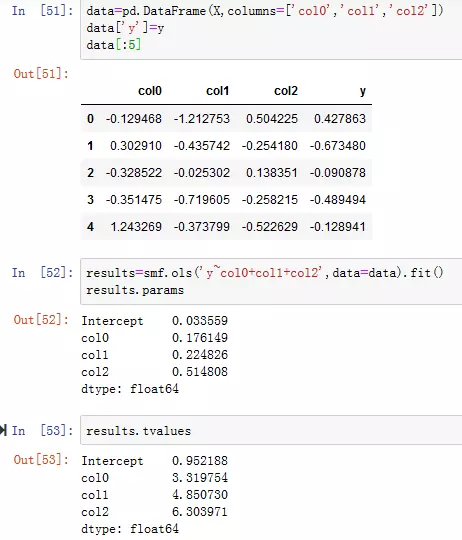
图5:statsmodels公式API和Patsy公式字符串
6.predict方法
观察statsmodels如何将结果作为带有DataFrame列名称的Series返回。使用公式和pandas对象时,我们也不需要使用add_constant。
给定新的样本外数据后,你可以根据估计的模型参数计算预测值(见图13-6)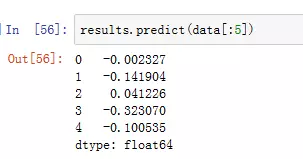
图6:predict方法
2 评估时间序列处理
statsmodels中的另一类模型用于时间序列分析。其中包括自回归过程,卡尔曼滤波和其他状态空间模型,以及多变量自回归模型。
让我们模拟一些具有自回归结构和噪声的时间序列数据(见图7)
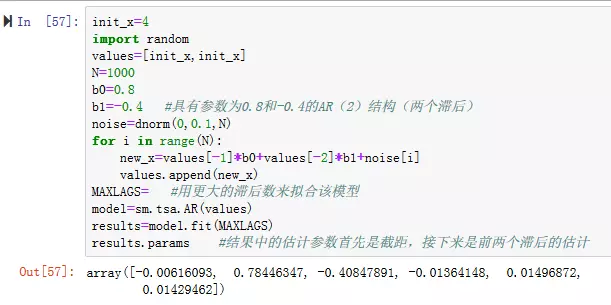
图7:模拟数据
相关文章:
《利用Python进行数据分析》13.3statsmodels介绍
为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



