AI 深度学习相关公式
一、单神经元神经网络


上图中就是单神经元, x1 就是一个特征,w1就是它对应的权重。
公式:
二、浅层神经网络
由于单神经元网络太简单,识别率不是很高。下面介绍稍微复杂一点的神经网络--浅层神经网络。


我们先计算出第一层的 3 个神经元的 a。然后再将这三个 a 当做 X 输入到第二层的神经元中计算。上面的 $ w^{[1]} $ 表示的是第一层的神经元关于输入层 x 的权重,所以,$w^{[1]}$ 是一个 3x3 的举证,因为第一层有 3 个神经元,每一个神经元都有 3 个特征输入。反向传播计算也是一样,先计算第二层的梯度 dw 和 db, 然后再向第一层传播,算出第一层 3 个神经元的dw 和 db。
浅层网络的前向传播计算
如下图,我们可以分别计算出第一层第一个神经元的 a。公式中的上脚标表示的是第几层,下角标表示的是该层的第几个神经元。

第一层有四个神经元,所以我们需要计算四次。但是如果有100个甚至是1000个神经元呢?一个一个的算效率太低了。根据我们前面所学,我们可以对它进行向量化。
要进行行向量,关键点是要将第一层的 4 个权重行向量组合成一个矩阵,如下图所示,$ w_1^{[1]T} $ 是一个行向量,表示第一层第一个神经元关于 3 个输入 x 的 3 个权重,$ w_2^{[1]T} $ 是第一层第二个神经元关于 3 个输入 x 的 3 个权重。四个这样的行向量组成一个 4 * 3 的矩阵。

由之前我们学的矩阵相乘的知识可得,每一个权重行向量都会与特征列向量 x 相乘,如下图所示:

所以,最终上面的 4 组式子就被向量化成了下面的这组式子--它一次性把第一层所有神经元的 a 都给计算出来了(无论有多少个神经元)。下面的 \(w^{[1]}\) 表示的是由 4 个权重行向量组合成的 4*3 (一个神经元对应三个特征值得权重如单神经元网络学的那样)的矩阵;\(b^{[1]}\) 是一个列向量,它包含了 4 个神经元相关的 4 个偏置b。
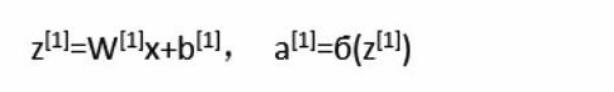
同理,下面这组式子把第二层的 $a^{[2]}$ 给计算出来了。和上面的式子是一样的,只不过 x 变成了 $a^{[1]}$ 。
上面的式子是适用于计算单训练样本的,但是训练神经网络要需要很多的样本,下面的代码用于计算多训练样本。下面的 m 表示训练样本的数量,for 循环遍历了每一个训练样本。
上面的代码是对的,但是效率太低。我们应该也把它给向量化了,把 for循环去除掉。想要向量化它们,关键点也是在于把每一个样本的特征列向量 x 组合成一个矩阵。如下图所示:
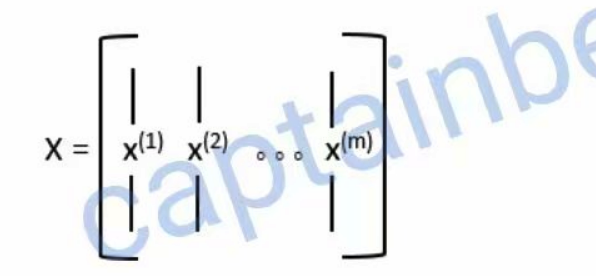
这样一来,上面的 for 循环代码就可以向量化成如下形式: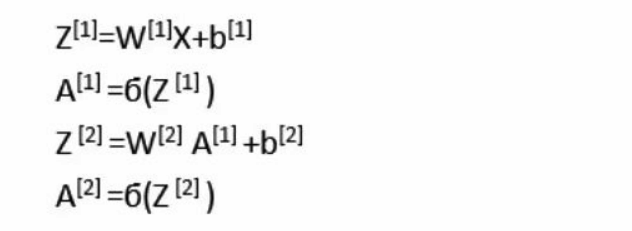
即:如果为单个样本则, \(W^{[1]}\) (43) x(31), 如果为多个样本,样本数为 m,则矩阵为 \(W^{[1]}\) (43) x(3m),
由前面文章所介绍的向量化知识可得,计算后的结果 Z 和 A 也是矩阵。
矩阵中的每一个列向量对应于一个样本。例如 \(z^{[1] (1)}\) 是第一个样本第一层的z。 \(z^{[1] (2)}\) 是第二个样本第一层的a。
得到最后一层的 A 后(也就是\(A^{[2]}\) ),我们可以通过下面的式子计算成本。和之前的单神经元网络是一样的。
反向传播计算
多训练样本公式:

三、深度神经网络

深度神经网络前向传播的计算形式和浅层神经网络是一样的,依然是利用下面两个经典的计算公式:
g代表激活函数,每一层的激活函数都可以是不同的。
反向传播利用的是下面的四个计算公式:

为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



