AI 深度学习之核对矩阵的维度

在编写深度神经网络程序时，出现的很多问题都是由于矩阵的维度不对引起的，而且这个问题非常难查。而且 python 有时候还会改变矩阵的维度（如广播化），所以我们要经常核对矩阵的维度，使之与我们预料中的一致。

一、核对矩阵

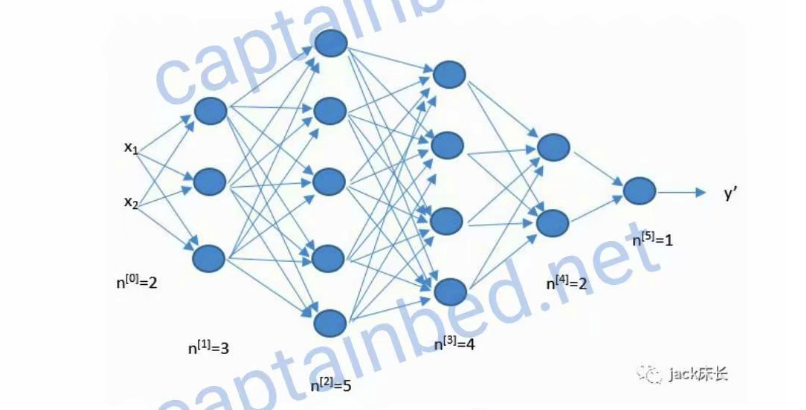
上面是一个五层的神经网络，输入层有 2 个元素，所以，\(n^{[0]}\)=2，第一层有 3 个元素，所以 \(n^{[1]}\)=3，其他层同理。

注意：\(n^{[0]}\) 层表示输入层，其他层都为神经元层。

下面列出单个训练样本时各变量的维度公式。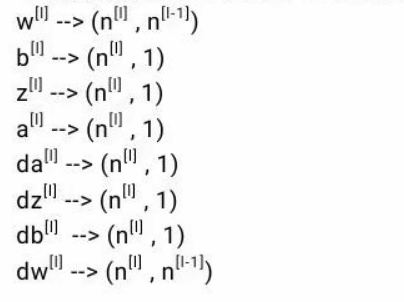

根据上面的公式，下面举例列出第一层的相关变量的维度。

那么当多个训练样本时维度公式又是怎样的呢？由以前学过的可知，我们会通过向量化来提升效率，例如我们会将每个样本的的特征 x 列向量，也就是 \(a^{[0]}\) 一个一个排起来，组成一个矩阵。

下面给出 m 个训练样本时的维度公式：

二、实战

# 该函数用于初始化所有层的参数w和b
def initialize_parameters_deep(layer_dims):
    """
    参数:
    layer_dims -- 这个list列表里面，包含了每层的神经元个数(包含输入层)。
    例如，layer_dims=[5,4,3]，表示第一层有5个神经元(输入层)，第二层有4个，最后一层有3个神经元

    返回值:
    parameters -- 这个字典里面包含了每层对应的已经初始化了的W和b。
    例如，parameters['W1']装载了第一层的w，parameters['b1']装载了第一层的b
    """
    np.random.seed(1)
    parameters = {}
    L = len(layer_dims) # 获取神经网络总共有几层

    # 遍历每一层，为每一层的W和b进行初始化
    for l in range(1, L):
        # 构建并随机初始化该层的W。由我前面的文章《1.4.3 核对矩阵的维度》可知，Wl的维度是(n[l] , n[l-1]) 
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l - 1]) / np.sqrt(layer_dims[l-1])
        # 构建并初始化b
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))

        # 核对一下W和b的维度是我们预期的维度
        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l - 1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))

    #就是利用上面的循环，我们就可以为任意层数的神经网络进行参数初始化，只要我们提供每一层的神经元个数就可以了。       
    return parameters

打印：

parameters = initialize_parameters_deep([5,4,3])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

结果：

W1 = [[ 0.72642933 -0.27358579 -0.23620559 -0.47984616  0.38702206]
 [-1.0292794   0.78030354 -0.34042208  0.14267862 -0.11152182]
 [ 0.65387455 -0.92132293 -0.14418936 -0.17175433  0.50703711]
 [-0.49188633 -0.07711224 -0.39259022  0.01887856  0.26064289]]
b1 = [[0.]
 [0.]
 [0.]
 [0.]]
W2 = [[-0.55030959  0.57236185  0.45079536  0.25124717]
 [ 0.45042797 -0.34186393 -0.06144511 -0.46788472]
 [-0.13394404  0.26517773 -0.34583038 -0.19837676]]
b2 = [[0.]
 [0.]
 [0.]]

为者常成，行者常至