机器学习实战之线性回归模型(一)
一、一元线性回归
概念
线性回归模型是利用线性拟合的方式来探寻数据背后的规律,如下图所示,就是通过搭建线性回归模型来寻找这些散点(也称样本点)背后的趋势线(也称回归曲线),而通过这个回归曲线我们就能进行一些简单的预测分析或因果关系分析。
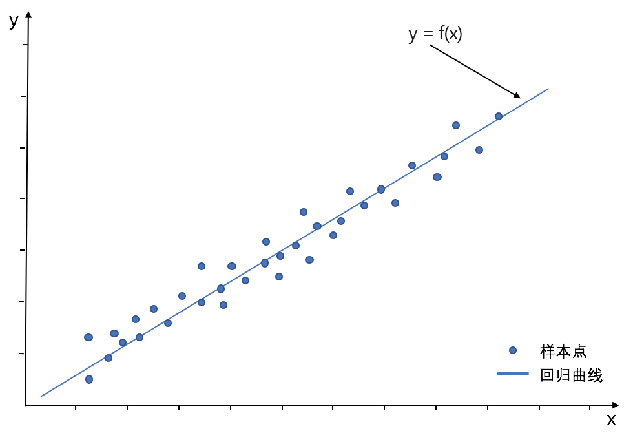
线性回归中,我们根据特征变量(也称自变量)来对反应变量(也称因变量)进行预测,根据特征变量的个数可将线性回归模型分为一元线性回归和多元线性回归。
通过一个特征变量:工作年限对收入进行预测,就属于一元线性回归;
通过多个特征变量:工作年限、行业、所在城市等对收入进行预测,就属于多元线性回归。
一元线性回归的数学原理
一元线性回归模型也称为简单线性回归模型,其形式可以通过如下公式表达:
y = a × x + b其中y为因变量,x为自变量,a表示回归系数,b表示截距。其中 y^i 为实际值, y ̂^i 为预测值,一元线性回归的目的就是拟合出一条线来使得预测值和实际值尽可能的接近,如果大部分点都落在拟合出来的线上,那么该线性回归模型则拟合较好。

我们通过两者差值的平方和(该和也称为残差平方和)来进行衡量,公式如下,其中 ∑ 为求和符号。此外,补充说明一句,在机器学习领域,该残差平方和也被称之为回归模型的损失函数(更多损失函数的相关知识点可以参考本书第9章的补充知识点)。
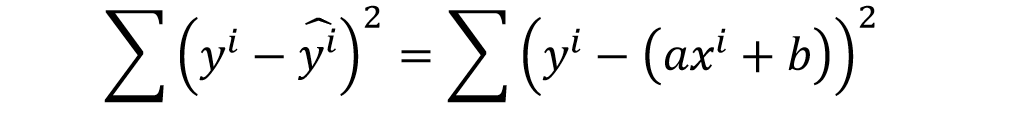
显然我们希望这个和越小越好,这样实际值和预测值就更加接近,而数学上求最小值的方法为求导数,当导数为0时,该残差平方和最小。
那么通过对残差平方和进行求导,然后令其导数为0便可以求得一元线性回归模型的系数a和截距b,这个便是一元线性回归的数学原理,学术上称其为最小二乘法。而在Python中就有专门的库来求解这里的系数a和截距b,而不需要我们去计算复杂的数学公式,这个我们将在下一节进行讲解。
一元线性回归的代码实现
通过Python的Scikit-learn库我们便可以轻松的搭建一元线性回归模型。
如果是通过之前讲过的Anaconda安装的Python的话,那么Scikit-learn库已经默认被安装好了。
为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



