Python:线性代数-向量-线性组合和张成 - 理论性定义 (四十五)

线性组合

一般来说，线性组合是指将标量与向量相乘，并将这些项相加。

例如：

如果 x、y 和 z 是变量，以及 \(a_1\)、\(a_2\) 和 \(a_3\) 是标量，以下方程将是线性组合：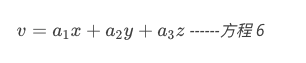

现在将它放到线性代数环境中。

我们的变量现在是向量：\(\vec{x}\)、 \( \vec{y}\) 和 \(\vec{z} \)是变量。
标量可以保持不变：\(a_1\)、\(a_2\) 和 \(a_3\) 。

标量与向量的线性组合成为新的向量：

线性组合可以只相加一次，也可以相加多次（如上面的方程 4 所示）。

向量与标量的线性组合一般记法为

什么是张成?

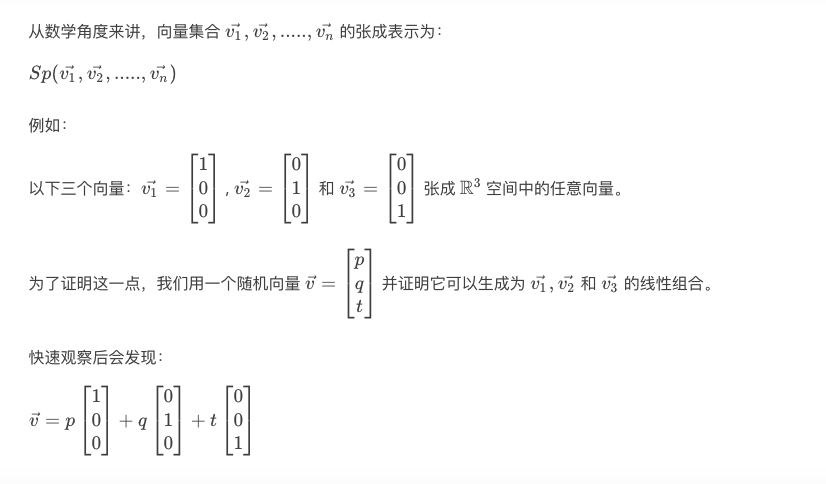
如果\( \vec{v_1}\), \(\vec{v_2}\),....., \(\vec{v_n}\) \(\in\) \(\mathbb{R} \)， 那么，

这些向量的张成（有时候也称为线性张成）是指这些向量的所有可能的线性组合。

为者常成，行者常至