Python:线性代数-线性组合实战 Lab (五十一)

线性组合

在此 notebook 中，你将学习如何使用 python 软件包NumPy 及其线性代数子软件包 linalg 求解线性组合问题。此 Lab 旨在帮助你掌握要在神经网络中用到的线性代数知识。

确定向量的张成

在线性组合课程中，我们提到一组给定向量的线性组合可以实现的所有可能向量集合称为这两个向量的张成。假设有一对向量 ?⃗ 和 ?⃗ ，我们想要判断它们的张成中是否存在第三个向量 ?⃗ ，表示 ?⃗ 可以写成向量对 ?⃗ 和 ?⃗ 的线性组合。

可以表示为：
??⃗ +??⃗ =?⃗ (方程 1) ，其中 ?⃗ 和 ?⃗ 分别乘以标量 ? 和 ?，然后相加生成向量 ?⃗ 。

如果我们能够找到一组使方程 1 成立的标量 ? 和 ? ，那么 ?⃗ 位于 ?⃗ 和 ?⃗ 的张成内。否则，如果没有使方程 1 成立的标量 ? 和 ? ，那么 ?⃗ 不在它们的张成内。

我们可以使用 NumPy 的线性代数子软件包 linalg 以计算方式确定向量的张成。下面看一个示例。

如果向量的值如下所示：
\(\vec{v}\) = \(\begin{bmatrix} 1 \\3 \end{bmatrix} \) \(\vec{w}\) = \(\begin{bmatrix} 2 \\5 \end{bmatrix} \) \(\vec{t}\) = \(\begin{bmatrix} 4 \\11 \end{bmatrix} \)

上边的MD语法

\\(\vec{v}\\) = \\(\begin{bmatrix} 1 \\\\3 \end{bmatrix} \\)    
\\(\vec{w}\\) = \\(\begin{bmatrix} 2 \\\\5 \end{bmatrix} \\)   
\\(\vec{t}\\) = \\(\begin{bmatrix} 4 \\\\11 \end{bmatrix} \\)  

可以将 ??⃗ +??⃗ =?⃗ 重新写成：
a\(\begin{bmatrix} 1 \\3 \end{bmatrix} \) + b\(\begin{bmatrix} 2 \\5 \end{bmatrix} \) = \(\begin{bmatrix} 4 \\11 \end{bmatrix} \)

在线性代数课程中，你也许可以手动求解这个问题：使用简化的梯阵形式，并将方程 1 重写为增广矩阵。我们在下面提供了方程 1 的增广矩阵。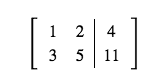

注意，增广矩阵的右侧包含向量 ?⃗ 。我们要判断此向量是否位于另外两个向量 ?⃗ 和 ?⃗ 的张成内。我们要检查其张成的另外两个向量组成了增广矩阵的左侧。

将向量\(\vec{v}\) 和 \(\vec{w}\) 可以抽象为在二维坐标的位置点(1,3)，(2,5)然后对向量进行伸缩即乘以标量，所有的变换集合表示向量的张成。

以计算方式确定张成

我们将使用 NumPy 的线性代数子软件包 (linalg) 以计算方式求解此问题，而不是手动求解。

以计算方式确定向量张成的步骤：

• 1、使用 import 方法使 NumPy Python 软件包可用
• 2、创建增广矩阵的右侧和左侧
  A：创建 NumPy 向量 ?⃗ 来表示增广矩阵的右侧。
  B：创建 NumPy 矩阵方法 ?? 来表示增广矩阵的左侧 （?⃗ 和 ?⃗ ）
• 3、使用 NumPy 的 linalg.solve 函数以计算方式检查向量的张成：求解使等式成立的标量。对于此 Lab ，你将使用你将在下方定义的 check_vector_span 函数。

对于下面的 Python 代码，你需要完成上面列出的第 1 和 2 步。

# Makes Python package NumPy available using import method
import numpy as np

# Creates matrix t (right side of the augmented matrix).
t = np.array([4, 11])

# Creates matrix vw (left side of the augmented matrix).
vw = np.array([[1, 2], [3, 5]])

# Prints vw and t
print("\nMatrix vw:", vw, "\nVector t:", t, sep="\n")

Matrix vw:
[[1 2]
[3 5]]

Vector t:
[ 4 11]

TODO：使用 linalg.solve 函数检查向量的张成

你将使用 NumPy 的 linalg.solve 函数检查向量 ?⃗ 是否位于另外两个向量 ?⃗ 和 ?⃗ 的张成内。要完成此任务，你需要将你的代码插入在以下代码单元格中定义的函数 check_vector_span 中。

• 使用 linalg.solve 函数求解使上述方程 1 成立的标量(vector_of_scalars) ，仅在要检查的向量 (vector_to_check) 位于其他向量 (set_of_vectors) 的张成内时才成立。
• 否则，向量 (vector_to_check) 不在张成内，并且返回一个空向量。

以下是各个参数和所返回变量的定义，可以帮助你完成此任务。

函数参数：

• set_of_vectors 是增广矩阵的左侧。该参数表示你要检查其张成的向量集合（例如 ?⃗ 和 ?⃗ ）。
• vector_to_check 是增广矩阵的右侧。该参数表示检查是否位于向量 set_of_vectors 的张成内的向量。

返回的变量：

• vector_of_scalars 包含将求解方程组的标量，前提是所检查的向量位于向量组的张成内。否则，它将是一个空向量。

对于以下 Python 代码，你需要完成以计算方式确定向量张成部分的第 3 步。在以下代码中（请参阅 TODO:），你需要将下面的 None 替换成使用 linalg.solve 函数求解标量 (vector_of_scalars) 的代码。

def check_vector_span(set_of_vectors, vector_to_check):
    # Creates an empty vector of correct size
    vector_of_scalars = np.asarray([None]*set_of_vectors.shape[0])

    # Solves for the scalars that make the equation true if vector is within the span
    try:
        # TODO: Use np.linalg.solve() function here to solve for vector_of_scalars
        vector_of_scalars = np.linalg.solve(set_of_vectors, vector_to_check)
        if not (vector_of_scalars is None):
            print("\nVector is within span.\nScalars in s:", vector_of_scalars)
    # Handles the cases when the vector is NOT within the span   
    except Exception as exception_type:
        if str(exception_type) == "Singular matrix":
            print("\nNo single solution\nVector is NOT within span")
        else:
            print("\nUnexpected Exception Error:", exception_type)
    return vector_of_scalars

通过求解标量检查 check_vector_span
我们来看看 ?⃗ 是否位于向量 ?⃗ 和 ?⃗ 的张成内，并检查你在上面添加到 check_vector_span 函数中的代码。

注意：

• 添加了检查另外两组向量的代码（请参阅下面的其他向量）。
• 要运行代码：
  • 点击“保存”图标（上方菜单栏中的文件下方的磁盘图标）以保存你的内容。
  • 选择内核和重新启动并运行所有以运行代码。

第二组向量具有以下值和增广矩阵：

对于以下 Python 代码 ，你将检查在以计算方式确定向量张成部分的第 3 步创建的函数。

# Call to check_vector_span to check vectors in Equation 1
print("\nEquation 1:\n Matrix vw:", vw, "\nVector t:", t, sep="\n")
s = check_vector_span(vw,t)

# Call to check a new set of vectors vw2 and t2
vw2 = np.array([[1, 2], [2, 4]]) 
t2 = np.array([6, 12])
print("\nNew Vectors:\n Matrix vw2:", vw2, "\nVector t2:", t2, sep="\n")    
# Call to check_vector_span
s2 = check_vector_span(vw2,t2)

# Call to check a new set of vectors vw3 and t3
vw3 = np.array([[1, 2], [1, 2]]) 
t3 = np.array([6, 10])
print("\nNew Vectors:\n Matrix vw3:", vw3, "\nVector t3:", t3, sep="\n")    
# Call to check_vector_span
s3 = check_vector_span(vw3,t3)

Equation 1:
Matrix vw:
[[1 2]
[3 5]]

Vector t:
[ 4 11]

Vector is within span.
Scalars in s: [ 2. 1.]

New Vectors:
Matrix vw2:
[[1 2]
[2 4]]

Vector t2:
[ 6 12]

No single solution
Vector is NOT within span

New Vectors:
Matrix vw3:
[[1 2]
[1 2]]

Vector t3:
[ 6 10]

No single solution
Vector is NOT within span

通过求解标量检查 check_vector_span 的解决方案

以上代码的输出应该与下面的输出相符。
你将发现，对于方程 1 ??⃗ +??⃗ =?⃗ ，向量 ?⃗ 位于 ?⃗ 和 ?⃗ 的张成内，并且标量具有以下值： ?=2 ， ?=1 ：

2\(\begin{bmatrix} 1 \\3 \end{bmatrix} \) + 1\(\begin{bmatrix} 2 \\5 \end{bmatrix} \) = \(\begin{bmatrix} 4 \\11 \end{bmatrix} \)

还将发现，两组新向量 \(\vec{t2}\) 和 \(\vec{t3}\) 不在张成内，因此没有标量值可以求解方程。

方程组

我们在上面测试的所有情形都可以写成二元方程组，我们尝试求解使两个方程都成立的标量。对于方程组，标量 ? 变成 ? ，标量 ? 变成 ? 。

因此方程 1 ??⃗ +??⃗ =?⃗ 可以写成：

a\(\begin{bmatrix} 1 \\3 \end{bmatrix} \) + b\(\begin{bmatrix} 2 \\5 \end{bmatrix} \) = \(\begin{bmatrix} 4 \\11 \end{bmatrix} \) ，其中 ?=2 并且 ?=1

变成以下二元方程组：
? + 2? = 4，
3? + 5? = 11
其中 ?=2 并且 ?=1

注意：

• 向量 ?⃗ 和 ?⃗ 变成两个方程左侧的系数。
• 向量 ?⃗ 变成两个方程右侧的解。
• 在两个方程中，标量 ? 变成变量 ? ，标量 ? 变成 ? 。
• 每个方程都可以表示为二维图中的直线。

方程组的解始终是三种潜在情况之一。当向量位于张成内时，有一个解，如上面的示例所示。当向量位于张成内时，有一个解或无穷多解；当向量不在张成内时，无解。我们将分别介绍这三种情况。

情形 1 - 一个解

可以将方程 1 看做以下二元方程组：

$$\hspace{1cm} \begin{array}{rcl} x + 2y & = & 4 \ 3x + 5y & = & 11 \end{array}$$，其中 x = 2并且 y = 1

我们可以像确定向量 \(\vec{t}\) 的张成一样，求解 x 和 y 方程组。这意味着，当向量位于张成中时，方程组有一个解。用图形表示的话，这个唯一解是线相交的点（在下图中为红点）。

%matplotlib inline
import matplotlib.pyplot as plt
plt.plot([4,0],[0,2],'b',linewidth=3)
plt.plot([3.6667,0],[0,2.2],'c-.',linewidth=3)
plt.plot([2],[1],'ro',linewidth=3)
plt.xlabel('Single Solution')
plt.show()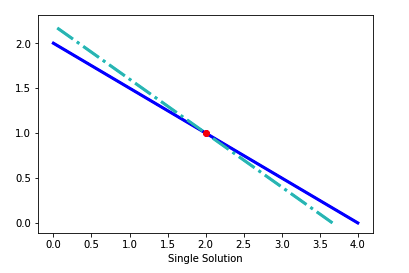

情形 2 - 无穷多解

第二种情形是标量值有无穷个，因为至少有两个方程是多余的。在我们的示例中，唯一的两个方程是多余的，它们表示同一条线（请参阅下图）。

第二种情形用 vw2 和 t2表示，其中：
\(\hspace{1cm} \begin{array}{rcl} x + 2y & = & 6 \ 2x + 4y & = & 12 \end{array}\)，其中任何 x和 y 都使该方程组成立，因为这两个方程是多余的。

import matplotlib.pyplot as plt
plt.plot([6,0],[0,3],'b',linewidth=5)
plt.plot([1,4,6,0],[2.5,1,0,3],'c-.',linewidth=2)
plt.xlabel('Redundant Equations')
plt.show()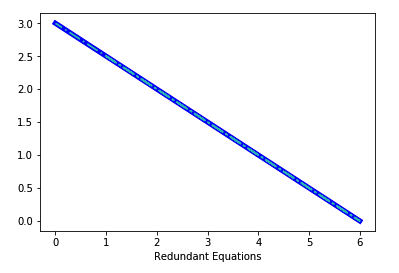

情形 3 - 无解

第三种情形是没有标量值可以同时求解所有方程。 在我们的示例中，唯一的两个方程表示为两条平行线，因为它们无解（请参阅下图）。

第三种情形用 ??3 和 ?3 表示，其中：
x + 2y = 6,
x + 2y = 10 , 其中没有任何 ? 和 ? 可以使方程组成立。

import matplotlib.pyplot as plt
plt.plot([10,0],[0,5],'b',linewidth=3)
plt.plot([0,6],[3,0],'c-.',linewidth=3)
plt.xlabel('No Solution')
plt.show()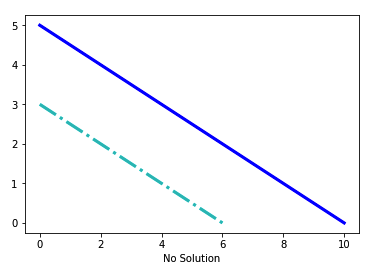

小结

对于 给定的向量组合 ?⃗ +??⃗ =?⃗ ，可以将向量先转为具体的向量坐标，然后再拆分为方程组，再解方程组即可。

为者常成，行者常至