Python:线性代数-矩阵乘法实战 Lab (五十三)
通过矩阵乘法进行货币换算
在此 notebook 中,你将使用矩阵乘法和 python 软件包 NumPy 解决一个货币换算问题。此演示旨在帮助你学习如何使用矩阵乘法解决更复杂的问题。
货币换算问题
这么多年来,你一共去过八个不同的国家/地区,并且留下了一些当地的货币。你打算再回到这八个国家/地区中的某个国家/地区,但是不确定要回到哪个国家/地区。
你打算看看哪个航线的机票最便宜。
为了做好行程准备,你需要将你的所有当地货币转换为你打算前往的国家/地区的货币。
因此,要仔细检查银行对你的货币换算结果,你想要计算八个国家/地区的每个国家/地区的总货币金额。
要计算换算结果,你首先需要导入包含每个国家/地区的货币换算率的矩阵。我们将使用的数据来自 Overview Matrix of Exchange Rates from Bloomberg Cross-Rates Overall Chart(2018 年 1 月 10 日)。
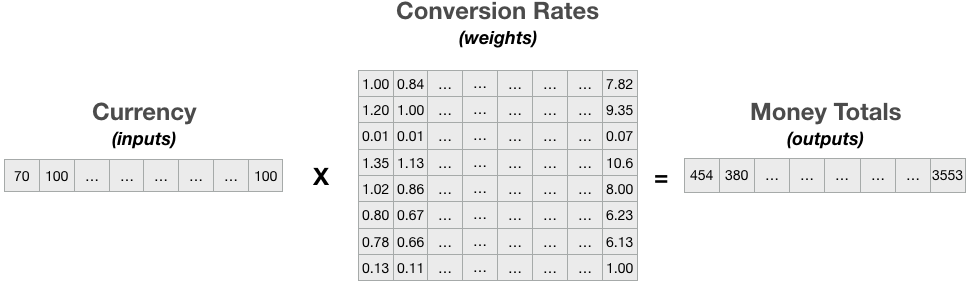
你可以将此问题看做接受一个输入向量(来自 8 个国家/地区的货币),并向这些输入应用 权重矩阵(换算率矩阵),以使用矩阵乘法和 NumPy 软件包生成 输出向量(每个国家/地区的货币总金额)。
编写货币换算问题代码
首先,你需要创建_输入向量_来存储表示八个国家/地区货币的 numpy 向量。首先导入 NumPy 软件包,然后使用该软件包根据列表创建向量。接着,将该向量转换为 pandas dataframe,以便在下面整洁地输出列标签,表示与货币金额相关的国家/地区。
import numpy as np
import pandas as pd
# Creates numpy vector from a list to represent money (inputs) vector.
money = np.asarray([70, 100, 20, 80, 40, 70, 60, 100])
# Creates pandas dataframe with column labels(currency_label) from the numpy vector for printing.
currency_label = ["USD", "EUR", "JPY", "GBP", "CHF", "CAD", "AUD", "HKD"]
money_df = pd.DataFrame(data=money, index=currency_label, columns=["Amounts"])
print("Inputs Vector:")
money_df.T
Inputs Vector:| USD | EUR | JPY | GBP | CHF | CAD | AUD | HKD | |
|---|---|---|---|---|---|---|---|---|
| Amounts | 70 | 100 | 20 | 80 | 40 | 70 | 60 | 100 |
接着,我们需要通过导入货币换算率矩阵创建权重矩阵。我们将使用 python 软件包 Pandas 快速读取该矩阵并相应地分配行和列标签。此外,我们定义一个变量 path 来定义货币换算矩阵的位置。下面的代码会导入该权重矩阵,将 DataFrame 转换为 numpy 矩阵,并显示其内容,以帮助你判断如何使用矩阵乘法解决该问题。
# Sets path variable to the 'path' of the CSV file that contains the conversion rates(weights) matrix.
path = %pwd
# Imports conversion rates(weights) matrix as a pandas dataframe.
conversion_rates_df = pd.read_csv(path+"/currencyConversionMatrix.csv",header=0,index_col=0)
# Creates numpy matrix from a pandas dataframe to create the conversion rates(weights) matrix.
conversion_rates = conversion_rates_df.values
# Prints conversion rates matrix.
print("Weights Matrix:")
conversion_rates_df
Weights Matrix:| USD | EUR | JPY | GBP | CHF | CAD | AUD | HKD | |
|---|---|---|---|---|---|---|---|---|
| USD-To | 1.0000 | 0.8364 | 111.3700 | 0.7404 | 0.9781 | 1.2548 | 1.2760 | 7.8218 |
| EUR-To | 1.1956 | 1.0000 | 133.1540 | 0.8852 | 1.1694 | 1.5002 | 1.5256 | 9.3517 |
| JPY-To | 0.0090 | 0.0075 | 1.0000 | 0.0066 | 0.0088 | 0.0113 | 0.0115 | 0.0702 |
| GBP-To | 1.3507 | 1.1297 | 150.4275 | 1.0000 | 1.3211 | 1.6949 | 1.7235 | 10.5649 |
| CHF-To | 1.0224 | 0.8551 | 113.8636 | 0.7569 | 1.0000 | 1.2829 | 1.3046 | 7.9969 |
| CAD-To | 0.7969 | 0.6666 | 88.7552 | 0.5900 | 0.7795 | 1.0000 | 1.0169 | 6.2335 |
| AUD-To | 0.7837 | 0.6555 | 87.2807 | 0.5802 | 0.7665 | 0.9834 | 1.0000 | 6.1299 |
| HKD-To | 0.1278 | 0.1069 | 14.2384 | 0.0947 | 0.1250 | 0.1604 | 0.1631 | 1.0000 |
上述_权重矩阵_提供了每个国家/地区之间的换算率。例如,在第 1 行第 1 列,值 1.0000 表示从美元到美元的换算率。在第 2 行第 1 列,值 1.1956 表示 1 欧元等于 1.1956 美元。在第 1 行第 2 列,值 0.8364 表示 1 美元仅等于 0.8364 欧元。
下面使用矩阵乘法计算了输出向量。numpy 软件包提供了将两个矩阵相乘(或向量与矩阵相乘)的函数 matmul。你将在下面找到适用于 AI 的矩阵乘法方程,其中输入向量(\(x_{1}...x_{n}\)) 乘以权重矩阵(\(w_{11}...w_{nm}\)) 以计算输出向量(\(y_{1}...y_{m}\))。
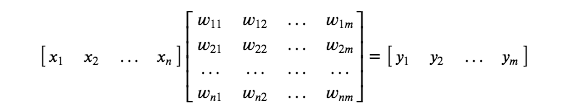
下面的示例矩阵乘法在输入和权重中将 n 设为 4,在权重和输出中将 m 设为 3。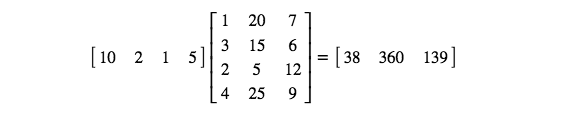
从上述示例可以看出,矩阵乘法生成的矩阵(输出向量)的行维度与第一个矩阵(输入向量)的一样,列维度将与第二个矩阵(权重矩阵)的一样。对于货币示例来说,输入矩阵和权重矩阵的列数一样,但是 AI 并非始终都如此。
TODO:矩阵乘法
在下面的空白处使用函数 matmul 将 money 和 conversion_rates 相乘,以计算向量 money_totals。之前我们在导入上述 Numpy 软件包时,使用了别名 np,因此在下面调用 matmul 函数时,确保使用别名 np。此外,确保选择“单元格” 和_“运行所有”_以检查你在下面插入的代码。
# TODO 1.: Calculates the money totals(outputs) vector using matrix multiplication in numpy.
money_totals = np.matmul(money, conversion_rates)
# Converts the resulting money totals vector into a dataframe for printing.
money_totals_df = pd.DataFrame(data = money_totals, index = currency_label, columns = ["Money Totals"])
print("Outputs Vector:")
money_totals_df.T
Outputs Vector:| USD | EUR | JPY | GBP | CHF | CAD | AUD | HKD | |
|---|---|---|---|---|---|---|---|---|
| Money Totals | 454.277 | 379.96 | 50593.59 | 336.338 | 444.326 | 570.034 | 579.667 | 3553.307 |
通过矩阵乘法进行货币换算的解决方案
上面的输出应该与下面的 Money Totals 相符。结果可以解析为:将所有货币换算为美元 (USD) 等于 454.28 美元,将所有货币换算为欧元 (EUR) 等于 379.96 欧元,等等。

为者常成,行者常至
自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)



